类比是研究问题的常用方法。
（1）情境1：物体从静止开始下落，除受到重力作用外，还受到一个与运动方向相反的空气阻力 （k为常量）的作用。其速率v随时间t的变化规律可用方程 （①式）描述，其中 为物体质量， 为其重力。求物体下落的最大速率 。
（2）情境2：如图1所示，电源电动势为 ，线圈自感系数为 ，电路中的总电阻为 。闭合开关 ，发现电路中电流 随时间 的变化规律与情境1中物体速率 随时间 的变化规律类似。类比①式，写出电流 随时间 变化的方程；并在图2中定性画出 图线。
（3）类比情境1和情境2中的能量转化情况，完成下表。
情境1 |
情境2 |
物体重力势能的减少量 |
|
物体动能的增加量 |
|
电阻R上消耗的电能 |
如图所示，带正电的小球套在绝缘的长直杆上，球与杆之间的动摩擦因素为μ，匀强电场水平向右，将杆与竖直线分别成不同角度固定放置，让小球由静止释放后都沿杆运动距离s，当杆与竖直线的夹角为θ时，小球获得的末动能最大为E．现将杆竖直固定放置，为使小球由静止释放后获得的动能与前面的动能E相等，小球运动的距离
应是多少？
有些人员，如电梯修理员、牵引专家等，常需要知道绳（或金属线）中的张力T，可又不便到绳（或线）的自由端去测量．现某家公司制造了一种夹在绳上的仪表（图中B、C为该夹子的横截面）．测量时，只要如图示那样用一硬杆竖直向上作用在绳上的某点A，使绳产生一个微小偏移量a，借助仪表很容易测出这时绳对硬杆的压力F。现测得该微小偏移量为a=12 mm，BC间的距离为 2L=250mm，绳对横杆的压力为 F=300N，试求绳中的张力T.
图中滑块和小球的质量均为m，滑块可在水平放置的光滑固定导轨上自由滑动，小球与滑块上的悬点 由一不可伸长的轻绳相连，轻绳长为 ．开始时，轻绳处于水平拉直状态，小球和滑块均静止．现将小球由静止释放，当小球到达最低点时，滑块刚好被一表面涂有粘住物质的固定挡板粘住，在极短的时间内速度减为零，小球继续向左摆动，当轻绳与竖直方向的夹角 ＝60°时小球达到最高点．求：
1.从滑块与挡板接触到速度刚好变为零的过程中，挡板阻力对滑块的冲量；
2.小球从释放到第一次到达最低点的过程中，绳的拉力对小球做功的大小．
一个玻璃瓶质量是0.21kg，密度是2.6×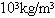
．在75cmHg大气压下，温度为27℃时，瓶里盛有空气200
．把瓶口向下推入池里的水中，使它自己停留在水中．该处水温为7℃，这时瓶内水面距池里水面的距离为多少？
我国发射的"嫦娥一号"探月卫星沿近似于圆形的轨道绕月飞行。为了获得月球表面全貌的信息，让卫星轨道平面缓慢变化。卫星将获得的信息持续用微波信号发回地球。设地球和月球的质量分别为
，地球和月球的半径分别为
，月球绕地球的轨道半径和卫星绕月球的轨道半径分别为
，月球绕地球转动的周期为
。假定在卫星绕月运行的一个周期内卫星轨道平面与地月连心线共面，求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间。（用
表示，忽略月球绕地球转动对遮挡时间的影）。