如图,在平面直角坐标系 中,抛物线 的顶点 在抛物线 上,直线 与抛物线 分别交于点 .
(1)求 的值;
(2)将 的纵坐标分别记为 ,设 ,若 的最大值为 ,则 的值是多少?
(3) 是 轴的正半轴上一点,且 的中点 恰好在抛物线 上.试探究:此时无论 为何负值,在 轴的负半轴上是否存在定点 ,使 总为直角?若存在,请求出点 的坐标;若不存在,请说明理由.

如图,C是AB的中点,AD=BE,CD=CE.求证:∠D=∠E.
利用网格线画图:如图,点A、B、C都在正方形网格的格点上.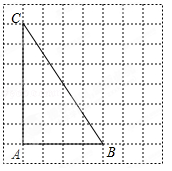
(1)在BC上找一点P,使PA=PB;
(2)在BC上找一点Q,使点Q到AB和AC的距离相等.
在如图所示的正方形网格中,点A、B、C在小正方形的顶点上.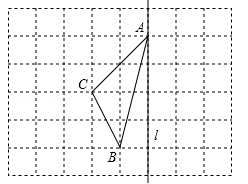
(1)在图中画出与△ABC关于直线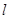 成轴对称的△AB′C′;
成轴对称的△AB′C′;
(2)线段C C′被直线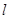 .
.
某居民统计了家里的用水量x(立方米)与应缴水费w(元)之间的关系如下表所示.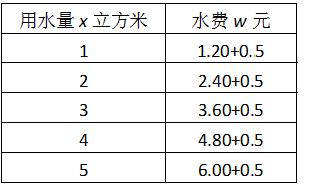
(1)写出用水量x(立方米)与水费w(元)之间的关系式.
(2)计算用水量是35立方米时的水费是多少元?
出租车司机小李某天下午的营运全是在东西走向的人民大街上行驶的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)若小李下午出发地记为0,他将最后一名乘客送抵目的地时距出发地点有多远?
(2)若汽车耗油量为0.41升/ 千米,这天下午小李共耗油多少升?