密闭容器内有一定质量的二氧化碳，当容器的体积 （单位： ）变化时，气体的密度 （单位： ）随之变化．已知密度 与体积 是反比例函数关系，它的图象如图所示，当 时， ．
（1）求密度 关于体积V的函数解析式；
（2）若 ，求二氧化碳密度 的变化范围．
甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同，每天甲、乙两人共加工35个零件，设甲每天加工x个.直接写出乙每天加工的零件个数（用含x的代数式表示）；
求甲、乙每天各加工多少个
根据市场预测估计，加工A型零件所获得的利润为m元/ 件（3≤m≤5），加工B型零件所获得的利润每件比A型少1元。求每天甲、乙加工的零件所获得的总利润P（元）与m的函数关系式，并求P的最大值、最小值.
如图（11），一次函数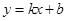
的图象与反比例函数
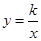的图象交于
、
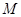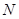两点。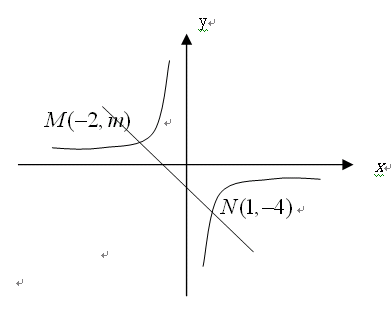
求反比例函数的解析式；
求一次函数的解析式；
根椐图象直接写出使反比例函数的值小于一次函数的值的
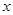的取值范围。
2009年，财政部发布了“家电下乡”的政府补贴资金政策，对农民购买手机等四类家电给予销售价格13﹪的财政补贴，以提高农民的购买力. 某公司为促进手机销售，推出A、B、C三款手机，除享受政府补贴，另外每部手机赠送120元话费. 手机价格如下表：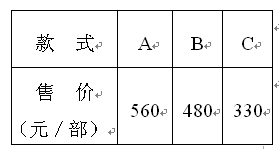
王强买了一部C款手机，他共能获得多少优惠？
王强买回手机后，乡亲们委托他代买10部手机，设所购手机的总售价为
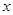元，两项优惠共
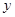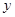元，请写出关于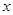的函数关系式；这时，政府最多需付出补贴资金多少元？根据（2）中的函数关系式，
在右边图象中填上适当的数据.
如图（9），在△ABC 中，BD＝CD， DE⊥AB， DF⊥AC，E、F为垂足，DE＝DF，求证：△BED≌△CFD。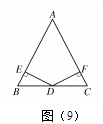
小明制作的风筝形状如图（8）所示，他根据DE=DF，EH＝FH，不用测量就知道∠Ｅ＝∠Ｆ，请你运用所学知识给予证明。