如图,在平面直角坐标系中,抛物线 与直线AB交于点 , .
(1)求该抛物线的函数表达式;
(2)点P是直线AB下方抛物线上的一动点,过点P作 轴的平行线交AB于点C,过点P作 轴的平行线交 轴于点D,求 的最大值及此时点P的坐标;
(3)在(2)中 取得最大值的条件下,将该抛物线沿水平方向向左平移5个单位,点E为点P的对应点,平移后的抛物线与 轴交于点F,M为平移后的抛物线的对称轴上一点.在平移后的抛物线上确定一点N,使得以点E,F,M,N为顶点的四边形是平行四边形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.

因式分解:4x2-12x+9
因式分解:8abx-12a2x2
如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
(1)求抛物线的解析式;
(2)求cos∠CAB的值和⊙O1的半径;
(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
如图1,在菱形ABCD中,AC=2,BD="2" 3 ,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.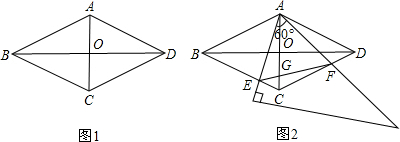
济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动,宁宁利用课余时间对某小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,宁宁将5月份各户居民的节水量统计整理如下统计图表:
| 节水量(米3) |
1 |
1.5 |
2.5 |
3 |
| 户数 |
50 |
80 |
100 |
700 |
(1)300户居民5月份节水量的众数,中位数分别是多少米3?
(2)扇形统计图中2.5米3对应扇形的圆心角为度;
(3)该小区300户居民5月份平均每户节约用水多少米3?