综合探究
如图1,在矩形 中( ),对角线 相交于点 ,点 关于 的对称点为 .连接 交 于点 ,连接 .
(1)求证: ;
(2)以点 为圆心, 为半径作圆.
①如图2, 与 相切,求证: ;
②如图3, 与 相切, ,求 的面积.

(本小题满分8分。其中(1)小题4分,(2)小题4分)
如图3:在正方形网格上有一个△ABC.
(1)作出△ABC关于直线MN的对称图形;
(2)若网格上最小正方形的边长为1,求△ABC的面积.
(本小题满分8分。其中(1)小题6分,(2)小题2分)如图2:在等边三角形△ABC中,BD平分∠ABC,延长BC到E,使CE=CD,连接D、E.
(1)小明同学说:“BD=DE”,他说得对吗?请你说明理由;
(2)小强同学说把“BD平分∠ABC”改成其它条件,也能得到同样的结论,你认为该如何改呢?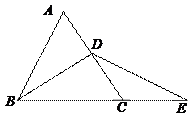
(本小题满分8分)小敏和小兰都想当节目主持人,但现在名额只有1个,为了能够选出1人参加,小丽想了一个办法:在三张卡片上分别写着3、-4、4,放入盒子里搅匀,随机抽取2张,若两张卡片上的数字之和为0,小敏当主持人,否则小兰当主持人,你认为这个游戏公平吗?用数据说明你的观点.
(本小题满分8分)阅读以下例题:解方程 =1
=1
解:①当5x≥0时,原方程可化为一元一次方程5x=1,它的解是 x= ;
;
②当5x<0时,原方程可化为一元一次方程-5x=1,它的解是 x=- .
.
所以原方程的解是x= 和x=-
和x=- .
.
请你模仿上面例题的解法,解方程 =2.
=2.
(本小题满分7分)
解不等式组 ,并将它的解集在数轴上标出来.
,并将它的解集在数轴上标出来.