(本小题满分12分)
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x(单位:分)如图2所示.
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
如图,AB是⊙O的直径,点C在⊙O上,AB=6,AC=5,求tanA的值.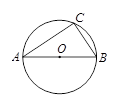
如图,四边形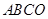 是平
是平 行四边形,
行四边形,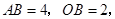 抛物线过
抛物线过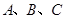 三点,与
三点,与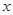 轴交于另一点
轴交于另一点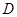 .一动点
.一动点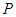 以每秒1个单位长度的速度从
以每秒1个单位长度的速度从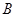 点出发沿
点出发沿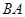 向点
向点 运动,运动到点
运动,运动到点 停止,同时一动点
停止,同时一动点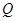 从点
从点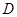 出发,以每秒3个单位长度的速度沿
出发,以每秒3个单位长度的速度沿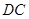 向点
向点 运动,与点
运动,与点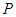 同时停止.
同时停止.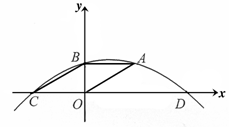
(1)求抛物线的解析式;
(2)若抛物线的对称轴与
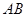 交于点
交于点
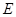 ,与
,与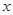 轴交于点
轴交于点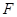 ,当点
,当点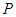 运动时间
运动时间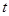 为何值时,四边形
为何值时,四边形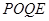 是等腰梯形?
是等腰梯形?(3)当
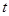 为何值时,以
为何值时,以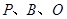 为顶点的三角形与以点
为顶点的三角形与以点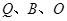 为顶点的三角形相似?
为顶点的三角形相似?
如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).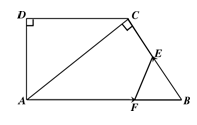
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交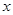 轴于
轴于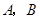 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点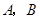 ,且其顶点
,且其顶点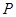 在⊙
在⊙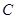 上.
上.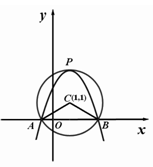
(1)求
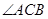 的大小;
的大小;(2)写出
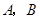 两点的坐标;
两点的坐标;(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点
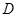 ,使线段
,使线段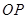 与
与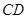 互相平分?若存在,求出点
互相平分?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某服装厂批发应季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示.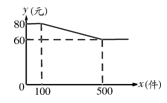
(1)请你直接写出当100<x≤500且x为整数时,y与x的函数关系式;
(2)一个批发商一次购进200件T恤衫,所花的钱数是多少元?
(其他费用不计);(3)若
 每件T恤衫的成本价是45元,当100<x≤500件( x为正整数)时,求服装厂所获利润w(元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?
每件T恤衫的成本价是45元,当100<x≤500件( x为正整数)时,求服装厂所获利润w(元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?