如图 ,
, 是两根柱子在同一灯光下的影子.
是两根柱子在同一灯光下的影子.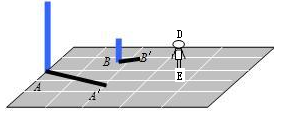
(1)请在图中画出光源的位置(用点P表示光源);
(2)在图中画出人物DE在此光源下的影子(用线段EF表示).
(本小题满分8分)
已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交 于点G,且∠EDF=∠ABE.
于点G,且∠EDF=∠ABE.
求证:(1)△DEF∽△BDE;
(2)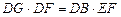 .
.
如图,在直角坐标平面内,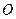 为原点,
为原点, 抛物线
抛物线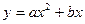 经过点
经过点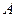 (
(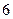 ,
,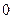 ),且顶点
),且顶点 (
( ,
,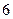 )在直线
)在直线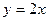 上.
上.
(1)求 的值和抛物线
的值和抛物线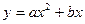 的解析式;
的解析式;
(2)如在线段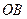 上有一点
上有一点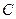 ,满足
,满足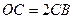 ,在
,在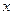 轴上有一点
轴上有一点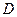 (
( ,
,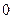 ),联结
),联结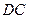 ,且直线
,且直线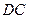 与
与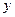 轴交于点
轴交于点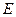 .
.
①求直线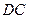 的解析式;
的解析式;
②如点M是直线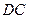 上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)
上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)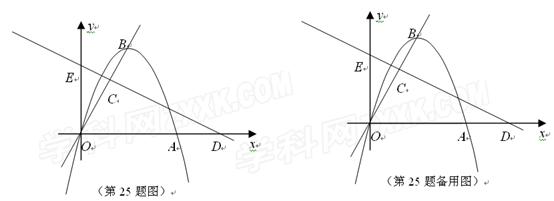
如图,在直角梯形ABCD中,AD∥BC,∠A=90o,BD⊥DC,BC=10cm,CD=6cm.在线段 、
、 上有动点
上有动点 、
、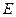 ,点
,点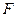 以每秒
以每秒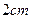 的速度,在线段
的速度,在线段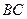 上从点B向点C匀速运动;同时点
上从点B向点C匀速运动;同时点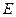 以每秒
以每秒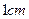 的速度,在线段
的速度,在线段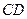 上从点C向点D匀速运动.当点
上从点C向点D匀速运动.当点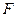 到达点C时,点
到达点C时,点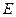 同时停止运动.设点
同时停止运动.设点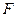 运动的时间为t(秒).
运动的时间为t(秒).
(1)求AD的长;
(2)设四边形BFED的面积为 ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;
(3)点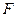 、
、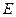 在运动过程中,如
在运动过程中,如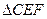 与
与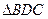 相似,求线段
相似,求线段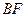 的长.
的长.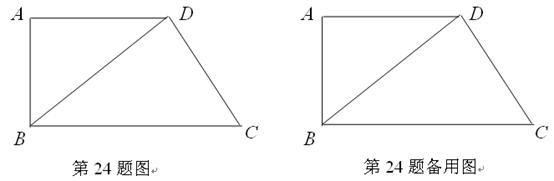
如图, 是⊙
是⊙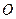 的弦,点D是弧AB的中点,过B作A
的弦,点D是弧AB的中点,过B作A B的垂线交AD的延长线于C.求证:AD=DC.
B的垂线交AD的延长线于C.求证:AD=DC.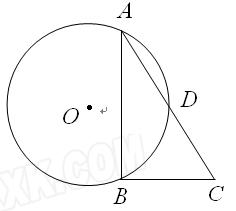
如图, 、
、 两地被一大山阻隔,汽车从
两地被一大山阻隔,汽车从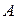 地到
地到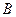 地须经过
地须经过 地中转.为了促进
地中转.为了促进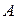 、
、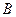 两地的经济发展,现计划开通隧道,使汽车可以直接从
两地的经济发展,现计划开通隧道,使汽车可以直接从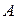 地到
地到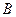 地.已知
地.已知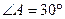 ,
,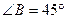 ,
,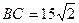 千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从
千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从 地到
地到 地需要多长时间?(参考数据:
地需要多长时间?(参考数据: )
)