阅读下列材料，然后解答问题．
经过正四边形（即正方形）各顶点的圆叫做这个正四边形的外接圆，圆心是正四边形的对称中心，这个正四边形叫做这个圆的内接正四边形．
如图，正方形ABCD内接于⊙O，⊙O的面积为S1，正方形ABCD的面积为S2．以圆心O为顶点作∠MON，使∠MON＝90°．将∠MON绕点O旋转，OM、ON分别与⊙O交于点E、F，分别与正方形ABCD的边交于点G、H．设由OE、OF、
及正方形ABCD的边围成的图形（阴影部分）的面积为S．
（1）当OM经过点A时（如图①），则S、S1、S2之间的关系为： （用含S1、S2的代数式表示）；
（2）当OM⊥AB于G时（如图②），则（1）中的结论仍然成立吗？请说明理由；
（3）当
旋转到任意位置时（如图③），则（1）中的结论仍然成立吗？请说明理由；
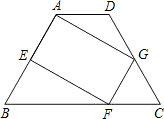
如图,在梯形
中,
,
．点
,
,
分别在边
,
,
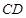上,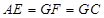
．
（1）求证：四边形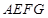
是平行四边形;
（2）当
时,求证：四边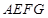形是矩形．
已知二次函数
．
（1）证明：不论
取何值,该函数图象与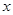
轴总有两个公共点;
（2）若该函数的图象与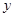
轴交于点(0,5),求出顶点坐标,并画出该函数图象．
解下列一元二次方程：
（1）
（2）
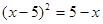
化简：
（
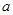≥0,
≥0）
如图所示，在平面直角坐标系中，Rt△OBC的两条直角边分别落在x轴、y轴上，且OB=1,OC=3,将△OBC绕原点O顺时针旋转90°得到△OAE，将△OBC沿y轴翻折得到△ODC，AE与CD交于点F.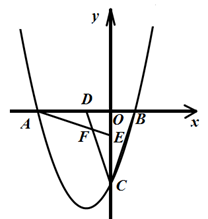
（1）若抛物线过点A、B、C, 求此抛物线的解析式;
（2）求△OAE与△ODC重叠的部分四边形ODFE的面积;
（3）点M是第三象限内抛物线上的一动点，点M在何处时△AMC的面积最大？最大面积是多少？求出此时点
的坐标.