小颖和小红两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：
（1）计算“3点朝上”的频率和“5点朝上”的频率；
（2）小颖说：“根据上述实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投掷600次，那么出现6点朝上的次数正好是100次”，小颖和小红的说法正确吗？为什么？

如图，在直角坐标系中，A（0，4），C（3，0）．
（1）①画出线段AC关于y轴对称线段AB；
②将线段CA绕点C顺时针旋转一个角，得到对应线段CD，使得AD∥x轴，请画出线段CD；
（2）若直线y=kx平分（1）中四边形ABCD的面积，请直接写出实数k的值．

化简求值：(1)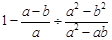，其中a＝－，b＝1
（2），其中满足.

计算：
(1)
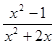
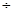
（2）

如图①，在□ABCD中，AB＝13，BC＝50，点P从点B出发，沿B—A—D—A运动．已知沿B—A运动时的速度为每秒13个单位长度，沿A—D—A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度. 若P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．

（1）当点P沿A—D—A运动时，求AP的长（用含t的代数式表示）．
（2）过点Q作QR//AB，交AD于点R，连结BR，如图②．在点P沿B—A—D运动过程中，是否存在线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分的情况，若存在，求出所有t的值，若不存在，请说明理由．
（3）设点C.D关于直线PQ的对称点分别为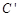、，在点P沿B—A—D运动过程中， 当//BC时，求t的值（直接写出结果）．