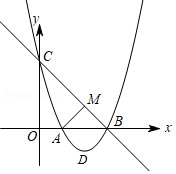
如图,在直角坐标系中,A(0,4),C(3,0).
(1)①画出线段AC关于y轴对称线段AB;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
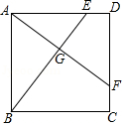
如图,正方形 ,点 , 分别在 , 上,且 , 与 相交于点 .
(1)求证: ;
(2)若 , ,求 的长.
某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动.为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
|
等级 |
频数 |
频率 |
|
优秀 |
21 |
|
|
良好 |
|
|
|
合格 |
6 |
|
|
待合格 |
3 |
|
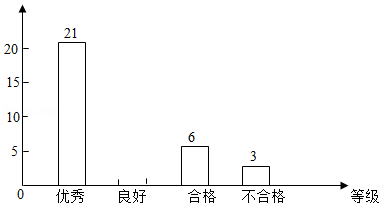
(1)本次调查随机抽取了 名学生;表中 , ;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
先化简,再求值: ,其中 .
计算: .
已知抛物线 过点 , 两点,与 轴交于点 , .
(1)求抛物线的解析式及顶点 的坐标;
(2)过点 作 ,垂足为 ,求证:四边形 为正方形;
(3)点 为抛物线在直线 下方图形上的一动点,当 面积最大时,求点 的坐标;
(4)若点 为线段 上的一动点,问: 是否存在最小值?若存在,求岀这个最小值;若不存在,请说明理由.