某企业为了适应市场需求，计划从2010年元月起，在每月固定投资5万元的基础上，元月份追加投资6万元，以后每月的追加投资额均为之前几个月投资额总和的20%，但每月追加部分最高限额为10万元. 记第n个月的投资额为
（1）求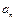
与n的关系式；
（2）预计2010年全年共需投资多少万元？（精确到0.01，参考数据：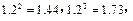
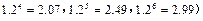
（本小题满分10分）选修4-4：坐标系与参数方程
直角坐标系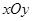
和极坐标系
的原点与极点重合，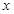
轴正半轴与极轴重合，单位长度相同，在直角坐标系下，曲线C的参数方程为
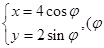为参数）。
（1）在极坐标系下，曲线C与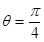射线
和射线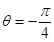
分别交于A，B两点，求
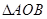的面积；
（2）在直角坐标系下，直线
的参数方程为
（
为参数），求曲线C与直线的交点坐标。
（本小题满分10分）选修4-1：几何证明选讲。如图，E是圆O内两弦AB和CD的交点F是AD延长线上一点，FG与圆O相切于点G，且EF=FG，求证：
（1）
；
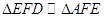（2）EF//BC。
（本小题满分12分）已知函数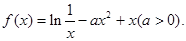
（1）若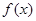
是单调函数，求
的取值范围；
（2）若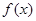有两个极值点
，证明：
（本小题满分12分）已知抛物线
的焦点为F，过点F作直线
与抛物线交于A，B两点，抛物线的准线与
轴交于点C。
（1）证明：
；
（2）求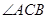
的最大值，并求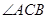取得最大值时线段AB的长。
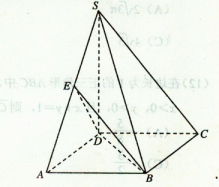
（本小题满分12分）如图，在四棱锥S—ABCD中，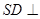
底面ABCD，底面ABCD是矩形，且
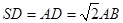，E是SA的中点。
（1）求证：平面BED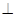
平面SAB；
（2）求平面BED与平面SBC所成二面角（锐角）的大小。