(选修4-1 几何证明选讲)
如图,已知:C是以AB为直径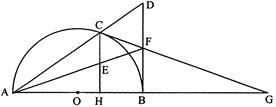 的半圆O上一点,
的半圆O上一点,
CH⊥AB于点H,直线AC与过B点的切线相交于
点D,E为CH中点,连接AE并延长交BD于点F,
直线CF交直线AB于点G.
(Ⅰ)求证:F是BD的中点;
(Ⅱ)求证:CG是⊙O的切线.
已知连续型随机变量 的概率密度函数
的概率密度函数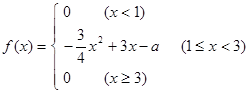 ,
,
(1)求常数 的值,并画出
的值,并画出 的概率密度曲线;
的概率密度曲线;
(2)求 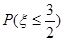 .
.
甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为 ;乙用这枚硬币掷2次,记正面朝上的次数为
;乙用这枚硬币掷2次,记正面朝上的次数为 。
。
(1)分别求 与
与 的期望;
的期望;
(2)规定:若 ,则甲获胜;若
,则甲获胜;若 ,则乙获胜,分别求出甲和乙获胜的概率.
,则乙获胜,分别求出甲和乙获胜的概率.
为了考察某种中药预防流感效果,抽样调查40人,得到如下数据:服用中药的有20人,其中患流感的有2人,而未服用中药的20人中,患流感的有8人。
(1)根据以上数据建立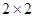 列联表;
列联表;
(2)能否在犯错误不超过0.05的前提下认为该药物有效?
参考
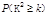 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
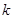 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
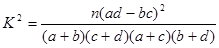 (
(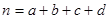 )
)
数学试题中有12道单项选择题,每题有4个选项。某人对每道题都随机选其
中一个答案(每个选项被选出的可能性相同),求答对多少题的概率最大?并求出此种情况下概
率的大小.(可保留运算式子)
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为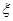 ,求
,求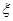 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.