数学试题中有12道单项选择题，每题有4个选项。某人对每道题都随机选其
中一个答案（每个选项被选出的可能性相同），求答对多少题的概率最大？并求出此种情况下概
率的大小.（可保留运算式子）
如图,已知抛物线C1:x2+by=b2经过椭圆C2: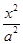
+
=1(a>b>0)的两个焦点.
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
设椭圆C1:
+
=1(a>b>0),抛物线C2:x2+by=b2.
(1)若C2经过C1的两个焦点,求C1的离心率;
(2)设A(0,b),Q（3
,
b）,又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B（0,
b）,且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
在平面直角坐标系xOy中,已知椭圆C1:
+
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(1)求椭圆C1的方程;
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(3)若点M的横坐标为
,直线l:y=kx+
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
≤k≤2时,|AB|2+|DE|2的最小值.
已知向量a="(1,2),b=(cos" α,sin α),设m=a+tb(t为实数).
(1)若α=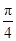
,求当|m|取最小值时实数t的值;
(2)若a⊥b,问:是否存在实数t,使得向量a-b和向量m夹角的余弦值为
,若存在,请求出t;若不存在,请说明理由.