设椭圆C1: +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.
(1)若C2经过C1的两个焦点,求C1的离心率;
(2)设A(0,b),Q(3 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0, b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
如图,已知:椭圆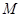 的中心为
的中心为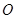 ,长轴的两个端点为
,长轴的两个端点为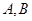 ,右焦点为
,右焦点为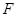 ,
,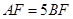 .若椭圆
.若椭圆 经过点
经过点 ,
, 在
在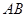 上的射影为
上的射影为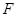 ,且△
,且△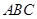 的面积为5.
的面积为5.
(Ⅰ)求椭圆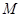 的方程;
的方程;
(Ⅱ)已知圆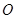 :
: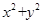 =1,直线
=1,直线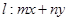 =1,试证明:当点
=1,试证明:当点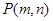 在椭圆
在椭圆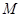 上
上
运动时,直线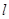 与圆
与圆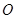 恒相交;并求直线
恒相交;并求直线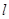 被圆
被圆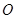 截得的弦长的取值范围.
截得的弦长的取值范围. 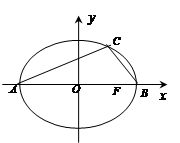
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离(即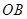 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为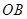 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为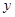 ,
,
(1)设∠CA1O =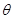 (rad),将y表示成
(rad),将y表示成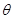 的函数关系式;
的函数关系式;
(2)请你设计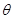 ,当角
,当角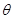 正弦值的大小是多少时,细绳总长
正弦值的大小是多少时,细绳总长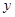 最小,并指明此时 BC应为多长。
最小,并指明此时 BC应为多长。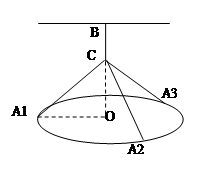
如图,直四棱柱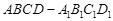 中,底面
中,底面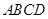 是直角梯形,
是直角梯形,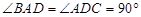 ,
,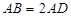 ,
,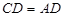 .
.
(1)求证: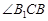 是二面角
是二面角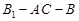 的平面角;
的平面角;
(2)在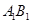 上是否存一点
上是否存一点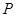 ,使得
,使得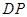 与平面
与平面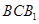 与平面
与平面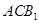 都平行?证明你的结论.
都平行?证明你的结论.
已知△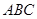 中,∠A,∠B,∠C的对边分别为
中,∠A,∠B,∠C的对边分别为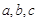 ,且
,且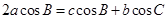 .
.
(1)求角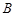 的大小;
的大小;
|
(2)设向量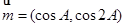 ,
,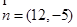 ,求当
,求当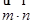 取最大值时,
取最大值时,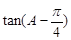 的值.
的值.
如下图所示是求某种运算的流程图,请你写出算法,并计算当n=6时,输出结果C的值.