已知向量 =(-cos(
=(-cos( -
- ),sin(-
),sin(- )),
)), =([cos(
=([cos( -
- )+sin(
)+sin( -
- )][cos(
)][cos( -
- )-sin(
)-sin( -
- )],2cos2
)],2cos2 -1).
-1).
(1)求证: ⊥
⊥
(2)设 =
= +(t2+3)
+(t2+3) ,
, =-k
=-k +t
+t ,
, =
= (
( ∈[-8,0]),若存在不等于0的实数
∈[-8,0]),若存在不等于0的实数 和
和 (
( ∈[1,2]),满足
∈[1,2]),满足 ⊥
⊥ ,试求
,试求 的最小值
的最小值 ,并求出
,并求出 的最小值.
的最小值.
(本小题满分12分)已知函数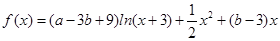 .
.
(1)当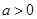 且
且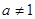 ,
,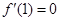 时,试用含
时,试用含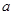 的式子表示
的式子表示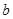 ,并讨论
,并讨论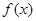 的单调区间;
的单调区间;
(2)若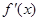 有零点,
有零点,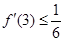 ,且对函数定义域内一切满足
,且对函数定义域内一切满足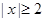 的实数
的实数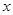 有
有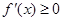 .
.
①求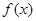 的表达式;
的表达式;
②当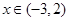 时,求函数
时,求函数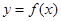 的图象与函数
的图象与函数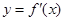 的图象的交点坐标.
的图象的交点坐标.
(本小题满分12分)已知椭圆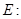
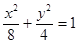 与直线
与直线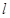 :
: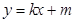 交于
交于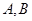 两点,
两点,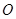 为坐标原点.
为坐标原点.
(Ⅰ)若直线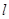 过椭圆的左焦点,且
过椭圆的左焦点,且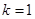 ,求
,求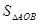 的面积;
的面积;
(Ⅱ)若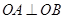 ,且直线
,且直线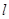 与圆
与圆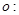
 相切,求圆
相切,求圆 的半径
的半径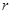 的值.
的值.
(本小题满分12分)已知函数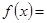
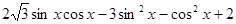 .
.
(1)当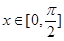 时,求
时,求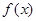 的值域;
的值域;
(2)若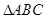 的内角
的内角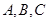 的对边分别为
的对边分别为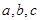 ,且满足
,且满足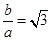 ,
,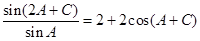 ,求
,求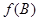 的值.
的值.
(本小题满分12分)已知等比数列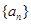 满足
满足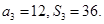
(1)求数列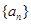 的通项公式;
的通项公式;
(2)求数列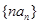 的前
的前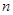 项和
项和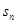 .
.
(本小题满分12分)已知圆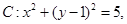 和直线
和直线 .
.
(1)求证:对 总有两个不同的交点
总有两个不同的交点 ;
;
(2)求弦 中点
中点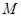 的轨迹方程,并说明其轨迹是什么曲线?
的轨迹方程,并说明其轨迹是什么曲线?