(本小题满分14分)
已知函数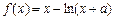 在
在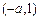 上单调递增,在
上单调递增,在 上单调递减.
上单调递减.
(Ⅰ)求实数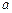 的值;
的值;
(Ⅱ)若关于 的方程
的方程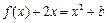 在
在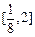 上恰有三个不相等的实数根,求实数
上恰有三个不相等的实数根,求实数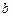 的取值范围;
的取值范围;
(Ⅲ)证明: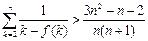 (
( ).(参考数据:
).(参考数据: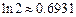 )
)
(本小题满分12分)
数列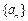 的前n项和为
的前n项和为 ,且
,且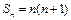 (
(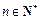 ).
).
(Ⅰ)求数列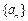 的通项公式;
的通项公式;
(Ⅱ)若数列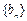 满足:
满足: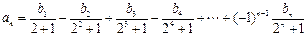 (
(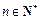 ),求数列
),求数列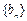 的通项公式;
的通项公式;
(Ⅲ)设 (
(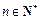 ),是否存在实数
),是否存在实数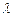 ,使
,使 得当
得当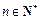 时,
时,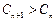 恒成立?若存在,求出实数
恒成立?若存在,求出实数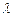 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题满分12分)
已知函数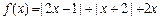 (
( ),
),
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)已知 ,命题p:关于x的不等式
,命题p:关于x的不等式 解集是空集;命题q:关于x的方程
解集是空集;命题q:关于x的方程 有实数根.若“p或q”为真,“p且q”为假,求实数m的取值
有实数根.若“p或q”为真,“p且q”为假,求实数m的取值 范围.
范围.
(本小题满分1 2分)
2分)
某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向 乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
(Ⅰ)求互换后两校派往两地区教师人数不变的概率;
(Ⅱ)求互换后A校教师派往甲地人数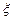 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分1 2分)
2分)
已知函数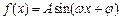 (
(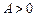 ,
,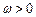 ,
,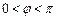
 )在
)在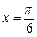 取得最大值2,方程
取得最大值2,方程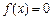 的两个根为
的两个根为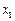 、
、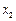 ,且
,且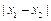 的最小值为
的最小值为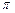 .
.
(Ⅰ)求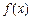 ;
;
(Ⅱ)将函数 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象.当
的图象.当 时,函数
时,函数 (m、n∈R)的值域是
(m、n∈R)的值域是 ,求实数m、n的值.
,求实数m、n的值.