为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:女生:
| 睡眠时间(小时) |
[4,5) |
[5,6) |
[6,7) |
[7,8) |
[8,9] |
| 人数 |
2 |
4 |
8 |
4 |
2 |
男生:
| 睡眠时间(小时) |
[4,5) |
[5,6) |
[6,7) |
[7,8) |
[8,9] |
| 人数 |
1 |
5 |
6 |
5 |
3 |
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取3人,求此3人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2x2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?
| |
睡眠时间少于7小时 |
睡眠时间不少于7小时 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
|
P(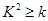 ) ) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.8879 |
10.828 |
( ,其中n=a+b+c+d)
,其中n=a+b+c+d)
设
和
是函数
的两个极值点.
(Ⅰ)求
和
的值;
(Ⅱ)求 的单调区间
如图,平面 平面 ,四边形 与 都是直角梯形, 分别为 中点.
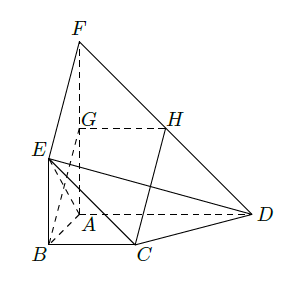
(Ⅰ)证明:四边形
是平行四边形;
(Ⅱ)
四点是否共面?为什么?
(Ⅲ)设
,证明:平面
平面
;
设进入某商场的每一位顾客购买甲种商品的概率为 ,购买乙种商品的概率为 ,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的。
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的3位顾客中至少有2位顾客既未购买甲种也未购买乙种商品的概率。
求函数 的最大值与最小值.
设 为实数,函数 .
(1)若 ,求 的取值范围;
(2)求 的最小值;
(3)设函数 ,直接写出(不需给出演算步骤)不等式 的解集.