如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都-优题课

题文

如图，平面 $A B E F ⊥$ 平面 $A B C D$ ，四边形 $A B E F$ 与 $A B C D$ 都是直角梯形， $∠ B A D = ∠ F A B = 90^{°}, B C = \frac{1}{2} A D, B E = \frac{1}{2} A F, G, H$ 分别为 $F A, F D$ 中点.

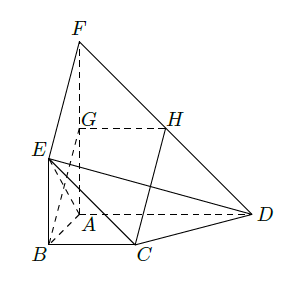
（Ⅰ）证明：四边形 $B C H G$ 是平行四边形；
（Ⅱ） $C, D, F, E$ 四点是否共面？为什么？
（Ⅲ）设 $A B = B E$ ，证明：平面 $A D E ⊥$ 平面 $C D E$ ；

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

解方程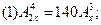

判断下列问题是排列问题还是组合问题？并计算出结果.
有八个质数：①从中任取两个数求它们的商可以有多少种不同的商？②从中任取两个求它的积，可以得到多少个不同的积？

判断下列问题是排列问题还是组合问题？并计算出结果.
高二年级数学课外小组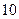人：①从中选一名正组长和一名副组长，共有多少种不同的选法？②从中选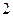名参加省数学竞赛，有多少种不同的选法？

判断下列问题是排列问题还是组合问题？并计算出结果.
高三年级学生会有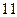人：①每两人互通一封信，共通了多少封信？②每两人互握了一次手，共握了多少次手？

是否存在正方形ABCD，它的对角线AC在直线x+y-2=0上，顶点B、D在抛物线y²=4x上?若存在，试求出正方形的边长；若不存在，试说明理由.

试卷网试题网古诗词网作文网范文网