从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表
如下：
| 分组（重量） |
 |
 |
 |
 |
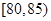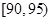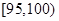| 频数（个） |
5 |
10 |
20 |
15 |
（1）根据频数分布表计算苹果的重量在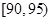的频率；
（2）用分层抽样的方法从重量在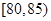和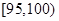的苹果中共抽取4个，其中重量在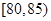的有几个？
（3）在（2）中抽出的4个苹果中，任取2个，求重量在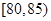和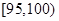中各有1个的概率．
(13分)一个同心圆形花坛，分为两部分，中间小圆部分种植绿色灌木，周围的圆环分为n(n≥3，n∈N)等份，种植红、黄、蓝三色不同的花，要求相邻两部分种植不同颜色的花.
⑴ 如图1，圆环分成的3等份为a1，a2，a3，有多少不同的种植方法？
如图2，圆环分成的4等份为a1，a2，a3，a4，有多少不同的种植方法？
⑵ 如图3，圆环分成的n等份为a1，a2，a3，……，an，有多少不同的种植方法？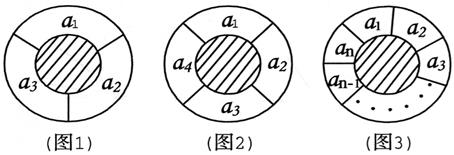
(12分) 已知数列
（n为正整数）是首项是a1，公比为q的等比数列.
(1)求和：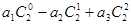
，
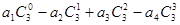
(2)由（1）的结果归纳概括出关于正整数n的一个结论，并加以证明.
(13分) 已知
的展开式中前三项的系数成等差数列．
（1）求n的值；
（2）求展开式中系数最大的项．
(12分) 由0，1，2，3，4，5这六个数字。
（1）能组成多少个无重复数字的四位数？
（2）能组成多少个无重复数字的四位偶数？
（3）能组成多少个无重复数字且被25个整除的四位数？
（4）组成无重复数字的四位数中比4032大的数有多少个？
已知z、w为复数，（1+3i）z为实数，w=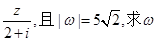
.