如图,已知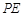 切⊙
切⊙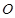 于点E,割线PBA交⊙
于点E,割线PBA交⊙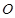 于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.
于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.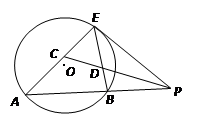
求证:
(Ⅰ)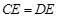 ;
;
(Ⅱ) .
.
(本小题满分12分)已知等差数列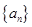 中,
中,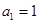 ,前
,前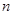 项和为
项和为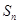 且满足条件:
且满足条件: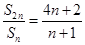 (
(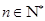 ).
).
(Ⅰ)求数列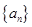 的通项公式;
的通项公式;
(Ⅱ)若数列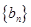 的前
的前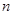 项和为
项和为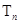 ,且有
,且有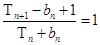 (
(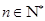 ),
),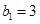 ,证明:数列
,证明:数列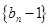 是等比数列;又
是等比数列;又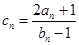 ,求数列
,求数列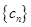 的前
的前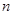 项和
项和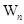 .
.
(本小题满分12分)为了进一步激发同学们的学习热情,某班级建立了理科、文科两个学习兴趣小组,两组的人数如下表所示.现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取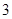 名同学进行测试.
名同学进行测试.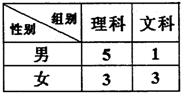
(Ⅰ)求从理科组抽取的同学中至少有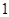 名女同学的概率;
名女同学的概率;
(Ⅱ)记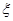 为抽取的
为抽取的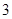 名同学中男同学的人数,求随机变量
名同学中男同学的人数,求随机变量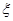 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)在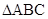 中,角
中,角 、
、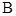 、
、 所对的边分别为
所对的边分别为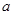 、
、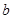 、
、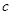 ,已知
,已知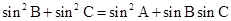 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若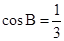 ,
,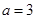 ,求
,求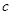 值.
值.
已知函数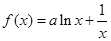
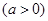 .
.
(Ⅰ)求函数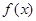 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若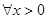 ,均有
,均有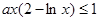 ,求实数
,求实数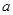 的取值范围.
的取值范围.
(Ⅲ)是否存在实数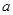 ,使得函数
,使得函数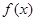 在
在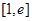 上的最小值为
上的最小值为 ?若存在试求出
?若存在试求出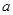 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分13分)已知椭圆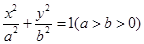 的离心率为
的离心率为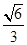 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线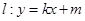 交椭圆于不同的两点
交椭圆于不同的两点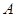 、
、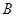 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线 分别切椭圆与圆
分别切椭圆与圆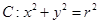 (其中
(其中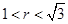 )于
)于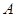 、
、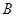 两点,求
两点,求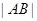 的最大值.
的最大值.