从某学校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的条形图.

(1)根据已知条件填写下面表格:
| 组别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 频数 |
|
|
|
|
|
|
|
|
(2)估计这所学校高三年级800名学生中身高在175cm以上(含175cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为同性别学生的概率是多少?
设函数 (其中
(其中 ).
).
(1) 当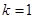 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;
(2) 当 时,函数
时,函数 在
在 上有且只有一个零点.
上有且只有一个零点.
点P是椭圆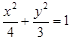 外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。
外的任意一点,过点P的直线PA、PB分别与椭圆相切于A、B两点。
(1)若点P的坐标为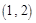 ,求直线
,求直线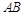 的方程。
的方程。
(2)设椭圆的左焦点为F,请问:当点P运动时,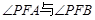 是否总是相等?若是,请给出证明。
是否总是相等?若是,请给出证明。
设数列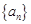 的前n项和为Sn,且
的前n项和为Sn,且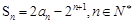 .
.
(1)求数列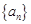 的通项公式;
的通项公式;
(2)令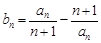 ,记数列
,记数列 的前
的前 项和为
项和为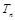 .求证:
.求证: .
.
如图,几何体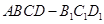 中,四边形
中,四边形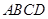 为菱形,
为菱形,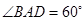 ,
,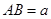 ,面
,面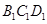 ∥面
∥面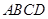 ,
,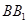 、
、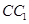 、
、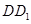 都垂直于面
都垂直于面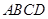 ,且
,且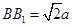 ,
,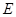 为
为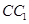 的中点,
的中点, 为
为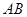 的中点.
的中点.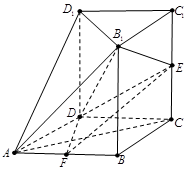
(1)求几何体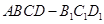 的体积;
的体积;
(2)求证: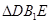 为等腰直角三角形;
为等腰直角三角形;
(3)求二面角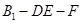 的大小.
的大小.
小明参加完高考后,某日路过一家电子游戏室,注意到一台电子游戏机的规则是:你可在1,2,3,4,5,6点中选一个,押上赌注a元。掷3枚骰子,如果所押的点数出现1次、2次、3次,那么原来的赌注仍还给你,并且你还分别可以收到赌注的1倍、2倍、3倍的奖励。如果所押的点数不出现,那么赌注就被庄家没收。
(1)求掷3枚骰子,至少出现1枚为1点的概率;
(2)如果小明准备尝试一次,请你计算一下他获利的期望值,并给小明一个正确的建议。