如图,某公司要在
两地连线上的定点
处建造广告牌
,其中
为顶端,
长35米,
长80米,设
在同一水平面上,从
和
看
的仰角分别为
和
.
(1)设计中
是铅垂方向,若要求
,问
的长至多为多少(结果精确到0.01米)?
(2)施工完成后,
与铅垂方向有偏差,现在实测得
,求
的长(结果精确到0.01米)?
设常数
,函数
若
=4,求函数
的反函数
;
根据
的不同取值,讨论函数
的奇偶性,并说明理由.
底面边长为2的正三棱锥
,其表面展开图是三角形
,如图,求△
的各边长及此三棱锥的体积
.
设函数
.
(1)当
(
为自然对数的底数)时,求
的最小值;
(2)讨论函数
零点的个数;
(3)若对任意
恒成立,求
的取值范围.
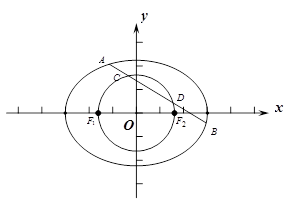
已知椭圆
经过点
,离心率为
,左右焦点分别为
.
(1)求椭圆的方程;
(2)若直线
与椭圆交于
两点,与以
为直径的圆交于
两点,且满足
,求直线
的方程.