已知函数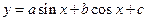 的图象上有一个最低点
的图象上有一个最低点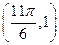 ,将图象上每个点的纵坐标不变,横坐标缩小到原来的
,将图象上每个点的纵坐标不变,横坐标缩小到原来的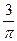 ,然后将所得图象向左平移一个单位得到
,然后将所得图象向左平移一个单位得到 的图象,若方程
的图象,若方程 的所有正根依次成为一个公差为3的等差数列,求
的所有正根依次成为一个公差为3的等差数列,求  的解析式.
的解析式.
(本小题满分14分)已知数列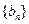 满足
满足 为
为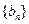 的前n项和。
的前n项和。
(1)求证:数列 是等比数列,并求
是等比数列,并求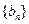 的通项公式;
的通项公式;
(2)如果对于任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)
在如图所示的多面体中,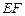 ⊥平面
⊥平面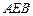 ,
, 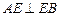 ,
,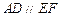 ,
,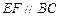 ,
, ,
, ,
,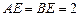 ,
, 是
是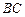 的中点.
的中点.
(1)求证: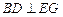 ;
;
(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.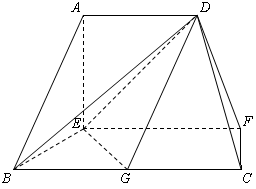
(本小题满分12分)
某工厂2011年第一季度生产的A、B、C、D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加四月份的一个展销会:
(1)问A、B、C、D型号的产 品各抽取多少件?
品各抽取多少件?
(2)从A、C型号的产品中随机的抽取3件,用 表示抽取A种型号的产品件数,求
表示抽取A种型号的产品件数,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分 分)已知函数
分)已知函数 ,
,
(1)求该函数的最小正周期和最小值;
(2)若 ,求该函数的单调递增区间。
,求该函数的单调递增区间。
(本题满分14分)
定义在(0,+∞)上的函数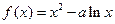 ,
, ,且
,且 在
在 处取极值。
处取极值。
(Ⅰ)确定函数 的单调性。
的单调性。
(Ⅱ)证明:当 时,恒有
时,恒有 成立.
成立.