(本小题满分14分)
在如图所示的多面体中,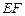 ⊥平面
⊥平面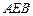 ,
, 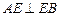 ,
,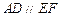 ,
,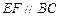 ,
, ,
, ,
,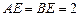 ,
, 是
是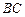 的中点.
的中点.
(1)求证: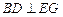 ;
;
(2)求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.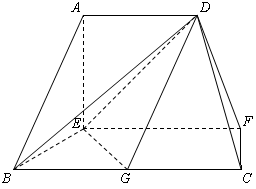
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以 后每年的维护费都比上一年增加2万元.
后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备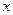 年的年平均污水处理费用
年的年平均污水处理费用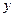 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水
如图所示是某班学生一次数学考试成绩的频率分布直方图,
其中纵轴表示学生数,观察图形,回答下列问题:
(1)全班有多少学生; (2)此次考试平均成绩大概是多少;
(3)不及格的人数有多少?占全班多大比例?
(4)如果80分以上的成绩为优良, 那么这个班的优良率为多少?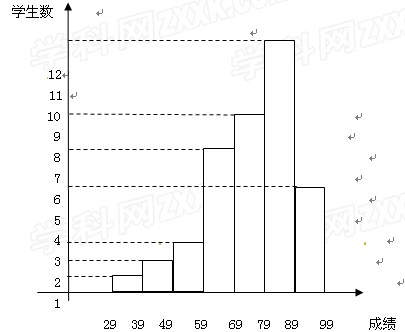
已知直线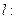
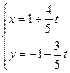 (
(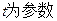 )与曲线C的极坐标方程:
)与曲线C的极坐标方程: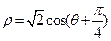 。
。
(1)求直线 与曲线C的直角坐标方程(极点与坐标原点重合,极轴与
与曲线C的直角坐标方程(极点与坐标原点重合,极轴与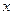 轴重合)
轴重合)
(2)求直线 被曲线C截得的弦长。
被曲线C截得的弦长。
袋中有大小相同的红、黄两种颜色的球各1个,从中任取1只,有放回地抽取3次.求:
(Ⅰ)3只颜色全相同的概率;
(Ⅱ)3只颜色不全相同的概率.
(Ⅲ)若摸到红球时得2分,摸到黄球时得1分,求3次摸球所得总分为5的概率。
若不等式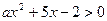 的解集是
的解集是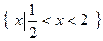 ,求不等式
,求不等式 的解集。
的解集。