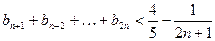如图,已知抛物线C1:x2+by=b2经过椭圆C2: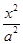 +
+ =1(a>b>0)的两个焦点.
=1(a>b>0)的两个焦点.
(1)求椭圆C2的离心率;
(2)设点Q(3,b),又M,N为C1与C2不在y轴上的两个交点,若△QMN的重心在抛物线C1上,求C1和C2的方程.
(本小题满分13分)设直线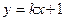 与圆
与圆 交于
交于 两点,且
两点,且 关于直线
关于直线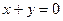 对称,
对称,
(Ⅰ)求 的值;
的值;
(Ⅱ)若直线 与
与 交
交 两点,是否存在实数
两点,是否存在实数 使得
使得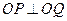 ,如果存在,求出
,如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分13分)已知 与
与 都是边长为
都是边长为 的等边三角形,且平面
的等边三角形,且平面 平面
平面 ,过点
,过点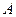 作
作 平面
平面 ,且
,且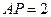 .
.
(Ⅰ)求直线 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅱ)平面 与底面
与底面 所成的二面角的余弦值.
所成的二面角的余弦值.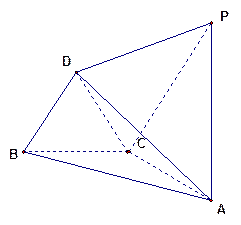
(本小题满分12分)(Ⅰ)在已知的坐标系中作出满足约束条件: ;
;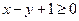 ;
;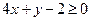 的可行性区域;
的可行性区域;
(Ⅱ)实数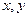 满足(Ⅰ)中约束条件,求目标函数
满足(Ⅰ)中约束条件,求目标函数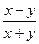 的取值范围.
的取值范围.
(本小题满分12分)已知四棱锥 的底面是边长为2的菱形,且
的底面是边长为2的菱形,且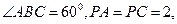
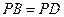 .
.
(Ⅰ)若O是AC与BD的交点,求证: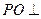 平面
平面 ;
;
(Ⅱ)若点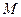 是
是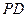 的中点,求异面直线
的中点,求异面直线 与
与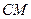 所成角的余弦值.
所成角的余弦值.
已知数列 满足
满足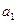 =-1,
=-1, ,数列
,数列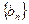 满足
满足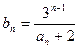
(1)求数列 的通项公式.
的通项公式.
(2)设数列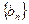 的前
的前 项和为
项和为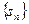 ,求证:当
,求证:当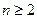 时,
时,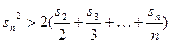 .
.
(3)求证:当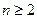 时,
时,