动点P在x轴与直线l：y＝3之间的区域（含边界）上运动，且点P到点F（0，1）和直线l的距离之和为4．
（Ⅰ）求点P的轨迹C的方程；
（Ⅱ）过点Q（0，－1）作曲线C的切线，求所作的切线与曲线C所围成的区域的面积
在平面四边形
中， 
。
（1）求
的长；
（2）若
，求
的面积。
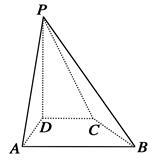
如图，在四棱锥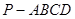
中，
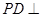平面
，
∥
，
．
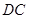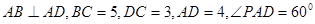（1）当正视方向与向量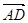
的方向相同时，画出四棱锥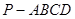的正视图（要求标出尺寸，并写出演算过程）；
（2）求三棱锥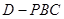
的体积．
选修4－5：不等式选讲
设函数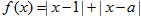
．
（1）若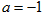
，解不等式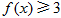
；
（2）如果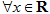
，
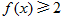，求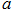
的取值范围．
选修4－4；坐标系与参数方程
在直角坐标系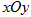
中，以O为极点，x轴正半轴为极轴建立极坐标系．曲线C的极坐标方程为
，M，N分别为C与x轴，y轴的交点．
（1）写出C的直角坐标方程，并求M、N的极坐标；
（2）设MN的中点为P，求直线OP的极坐标方程．
选修4－1：几何证明选讲
已知
中，
，D是外接圆劣弧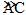
上的点（不与点A，C重合），延长BD至E．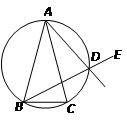
（1）求证：AD的延长线平分
CDE；
（2）若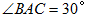
，中BC边上的高为2+
，求外接圆的面积．