(本小题满分12分)
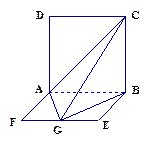 |
如图,ABCD是边长为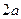 的正方形,ABEF是矩形,且二面角C
的正方形,ABEF是矩形,且二面角C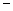 AB
AB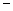 F是直二面角,
F是直二面角,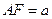 ,G是EF的中点, (Ⅰ)求证平面
,G是EF的中点, (Ⅰ)求证平面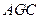 ⊥平面
⊥平面 ;
;
(Ⅱ)求GB与平面AGC所成角的正弦值.
(Ⅲ)求二面角B—AC—G的大小.
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数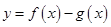 的极值;
的极值;
(Ⅱ)已知实数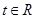 ,求函数
,求函数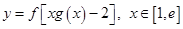 的值域.
的值域.
(本小题满分12分)已知函数 (其中
(其中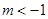 ),
),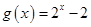 .
.
(Ⅰ)若命题“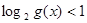 ”是真命题,求
”是真命题,求 的取值范围;
的取值范围;
(Ⅱ)设命题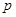 :
: ;命题
;命题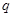 :
: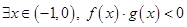 .若
.若 是真命题,求
是真命题,求 的取值范围.
的取值范围.
(本小题满分12分)设函数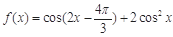 ,
,
(Ⅰ)求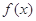 的最大值,并写出使
的最大值,并写出使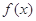 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知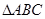 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若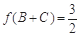 ,
,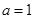 ,求
,求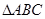 的面积的最大值.
的面积的最大值.
(本小题满分12分)设函数
(1)若 求
求 的单调区间;
的单调区间;
(2)若当 时,
时, ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知曲线 在点
在点 处的切线的斜率为1.
处的切线的斜率为1.
(1)若函数f(x)的图象在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)当 时,不等式
时,不等式 恒成立,求a的取值范围.
恒成立,求a的取值范围.