某果园要将一批水果用汽车从所在城市甲运至销售商所在城市乙。已知从城市甲到城市乙只有两条公路,且运费由果园承担。若果园恰能在约定日期(×月×日)将水果送到,则销售商一次性支付给果园20万元;若在约定日期前送到,每提前一天销售商将多支付给果园1万元。若在约定日期后运到,每迟到一天销售商将少支付给果园l万元。为保证水果新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送水果。已知下表内的信息:
| 统计信息 汽车行驶路线 |
不堵车的情况下到达 城市乙所需时间(天) |
堵车的情况下到达 城市乙所需时间(天) |
堵车的 概率 |
运费 (万元) |
| 公路1 |
2 |
3 |
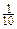 |
1.6 |
| 公路2 |
1 |
4 |
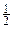 |
0.8 |
(1)记汽车走公路1时果园获得的毛利润为 (单位:万元),求
(单位:万元),求 的分布列和数学期望
的分布列和数学期望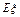 ;
;
(2)假设你是果园的决策者,你选择哪条公路运送水果有可能让果园获得的毛利润更多?
|
注:毛利润=销售商支付给果园的费用-运费
如图,四棱锥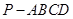 的底面是正方形,
的底面是正方形,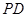 ⊥底面
⊥底面 ,点
,点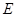 在棱
在棱 上.
上.
(1)求证:平面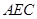 ⊥平面
⊥平面 ;
;
(2)当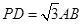 且
且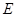 为
为 的中点时,求
的中点时,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”.每位社区居民可以在这三天中的任意一天参加任何一个讨论,也可以放弃任何一个讲座(规定:各个讲座达到预先设定的人数时称为满座).统计数据表明,各个讲座各天满座的概率如下表:
| 洗发水讲座 |
洗面奶讲座 |
护肤霜讲座 |
活颜营养讲座 |
面膜使用讲座 |
|
| 3月8日 |
 |
 |
 |
 |
 |
| 3月9日 |
 |
 |
 |
 |
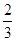 |
| 3月10日 |
 |
 |
 |
 |
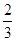 |
(1)求面膜使用讲座三天都不满座的概率;
(2)设3月9日各个讲座满座的数目为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知△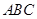 中,角
中,角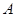 、
、 、
、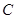 成等差数列,且
成等差数列,且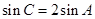 .
.
(1)求角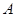 、
、 、
、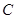 ;
;
(2)设数列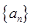 满足
满足 ,前
,前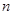 项为和
项为和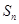 ,若
,若 ,求
,求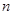 的值.
的值.
已知函数 .(1)求函数
.(1)求函数 的单调区间;
的单调区间;
(2)设函数 .若至少存在一个
.若至少存在一个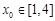 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆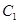 的中心在坐标原点,两个焦点分别为
的中心在坐标原点,两个焦点分别为 ,
,
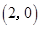 ,点
,点 在椭圆
在椭圆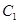 上,过点
上,过点 的直线
的直线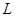 与抛物线
与抛物线 交于
交于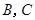 两点,抛物线
两点,抛物线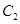 在点
在点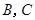 处的切线分别为
处的切线分别为 ,且
,且 与
与 交于点
交于点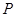 .
.
(1) 求椭圆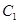 的方程;
的方程;
(2) 是否存在满足 的点
的点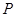 ? 若存在,指出这样的点
? 若存在,指出这样的点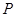 有几个(不必求出点
有几个(不必求出点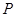 的坐标); 若不存在,说明理由.
的坐标); 若不存在,说明理由.