一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”．每位社区居民可以在这三天中的任意一天参加任何一个讨论，也可以放弃任何一个讲座（规定：各个讲座达到预先设定的人数时称为满座）．统计数据表明，各个讲座各天满座的概率如下表：
| |
洗发水讲座 |
洗面奶讲座 |
护肤霜讲座 |
活颜营养讲座 |
面膜使用讲座 |
| 3月8日 |
 |
|
|
|
 |
| 3月9日 |
|
|
|
|
 |
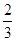| 3月10日 |
 |
|
|
|
|
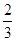（1）求面膜使用讲座三天都不满座的概率；
（2）设3月9日各个讲座满座的数目为
，求随机变量的分布列和数学期望．
已知函数
（1）当a=1时，解不等式
（2）若存在
成立，求a的取值范围．
在极坐标系中，曲线
的极坐标方程为
，现以极点
为原点，极轴为
轴的非负半轴建立平面直角坐标系，直线
的参数方程为
（
为参数）
（1）写出直线l和曲线C的普通方程；
（2）设直线l和曲线C交于A，B两点，定点P（—2，—3），求|PA|·|PB|的值．
如图，在△ABC中，CD是∠ACB的角平分线，△ADC的外接圆交BC于点E，AB=2AC
（1）求证：BE=2AD；
（2）当AC=3，EC=6时，求AD的长．
已知函数
函数
在
处取得极值1.
（1）求实数b，c的值；
（2）求
在区间[-2，2]上的最大值．
已知圆
的圆心在坐标原点
，且恰好与直线
相切，设点A为圆上一动点，
轴于点
，且动点
满足
，设动点的轨迹为曲线
（1）求曲线C的方程，
（2）直线l与直线l，垂直且与曲线C交于B、D两点，求△OBD面积的最大值．