已知圆
的圆心在坐标原点
，且恰好与直线
相切，设点A为圆上一动点，
轴于点
，且动点
满足
，设动点的轨迹为曲线
（1）求曲线C的方程，
（2）直线l与直线l，垂直且与曲线C交于B、D两点，求△OBD面积的最大值．
（本小题满分12分）
如图，在直三棱柱
中，
. 
（Ⅰ）求证：
∥平面
；
（Ⅱ）求证：
.
（本小题满分12分）
在△
中，角A、B、C所对的边分别为a，b，c，已知
，其中C为锐角．
（Ⅰ）求
的值；
（Ⅱ）当
时，求b及c的值.
（本小题满分14分）
已知函数
。
（1）求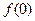
；
（2）探究
的单调性，并证明你的结论；
（3）若为奇函数，求满足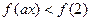
的
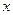的范围。
(本小题12分)
某商店按每件80元的价格，购进时令商品（卖不出去的商品将成为废品）1000件；市场调研推知：当每件售价为100元时，恰好全部售完；在此基础上当售价每提高1元时，销售量就减少5件；为获得最大利润，请你确定合理的售价，并求出此时的利润；
(本小题12分)已知二次函数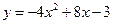
。
（1）指出图像的开口方向、对称轴方程、顶点坐标；
（2）画出它的图像，并说明其图像由
的图像经过怎样平移得来；
（3
）求函数的最大值或最小值；
（4）写出函数的单调区间（不必证明）。