设数列
满足
,其中
为实数.
(Ⅰ)证明:
对任意
成立的充分必要条件是
.
(Ⅱ)设
,证明:
;
(Ⅲ)设
,证明:
(本小题满分14分)如图,建立平面直角坐标系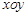 ,
,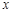 轴在地平面上,
轴在地平面上,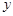 轴垂直于地
轴垂直于地
平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程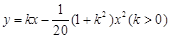 表示的曲线上,其中
表示的曲线上,其中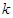 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标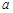 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.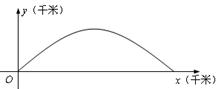
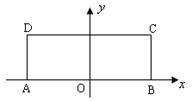
(本小题满分14分)已知长方形 ,
,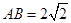 ,
,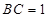 ,以
,以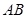 的中点
的中点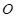 为
为
原点建立如图所示的平面直角坐标系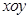 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中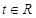 ,探究
,探究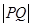 的最
的最
小值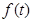 。
。
(本小题满分14分)如图所示,在四棱锥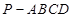 中,
中,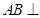 平面
平面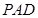 ,
,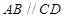 ,
,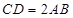 ,
,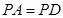 ,
, 是
是 的中点.
的中点.
(1)证明: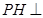 平面
平面 ;
;
(2)若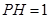 ,
,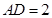 ,
,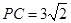 ,求二面角
,求二面角 的正切值.
的正切值.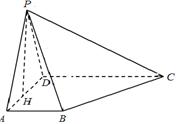
(本小题满分12分)已知数列{an}的前n项和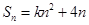 ,
,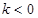 ,且Sn的最大值为8.
,且Sn的最大值为8.
(1)确定常数k的值,并求通项公式an;
(2)求数列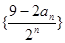 的前n项和Tn。
的前n项和Tn。
(本小题满分12分)函数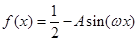 (
(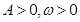 )的最大值为1,对任意
)的最大值为1,对任意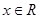 ,有
,有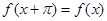 。
。
(1)求函数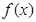 的解析式;
的解析式;
(2)若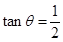 ,其中
,其中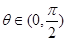 ,求
,求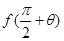 的值。
的值。