(本小题满分14分)如图,建立平面直角坐标系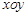 ,
,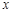 轴在地平面上,
轴在地平面上,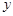 轴垂直于地
轴垂直于地
平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程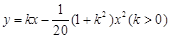 表示的曲线上,其中
表示的曲线上,其中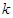 与发射方向有关,炮的射程是指炮弹落地点的横坐标.
与发射方向有关,炮的射程是指炮弹落地点的横坐标.
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标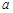 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.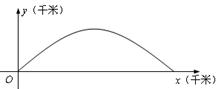
.(本小题满分12分)
已知集合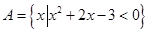 ,
, ,
,
(1)在区间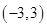 上任取一个实数
上任取一个实数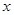 ,求“
,求“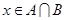 ”的概率;
”的概率;
(2)设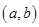 为有序实数对,其中
为有序实数对,其中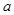 是从集合
是从集合 中任取的一个整数,
中任取的一个整数,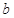 是从集合
是从集合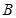 中任取的一个整数,求“
中任取的一个整数,求“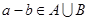 ”的概率.
”的概率.
、(本小题满分14分)设函数
(Ⅰ)求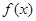 的单调区间;
的单调区间;
(Ⅱ)当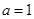 时,若方程
时,若方程 在
在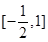 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,
(本小题满分14分) 已知数列 满足:
满足:
(Ⅰ)探究数列 是等差数列还是等比数列,并由此求数列
是等差数列还是等比数列,并由此求数列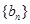 的通项公式;
的通项公式;
(Ⅱ)求数列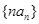 的前n项和
的前n项和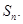
(本小题满分14分)
已知汕头市某学校高中部某班共有学生50人,其中男生30人,女生20人,班主任决定用分层抽样的方法在自己班上的学生中抽取5人进行高考前心理调查。
(Ⅰ)若要从这5人中选取2人作为重点调查对象,求至少选取1个男生的概率;
(Ⅱ)若男学生考前心理状态好的概率为0.6,女学生考前心理状态好的概率为0.5, 表示抽取的5名学生中考前心理状态好的人数,求P(
表示抽取的5名学生中考前心理状态好的人数,求P( =1)及E
=1)及E .
.
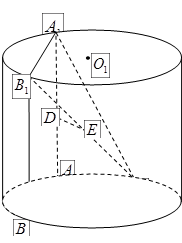
(本小题满分14分)如图, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆 的直径,
的直径,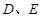 分别是
分别是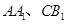 的中点,DE⊥面CBB1.
的中点,DE⊥面CBB1.
(Ⅰ)证明:DE //面ABC;
(Ⅱ)求四棱锥 与圆柱
与圆柱 的体积比;
的体积比;
(Ⅲ)若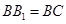 ,求
,求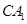 与面
与面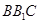 所成角的正弦值.
所成角的正弦值.