(本小题满分14分) 已知数列 满足:
满足:
(Ⅰ)探究数列 是等差数列还是等比数列,并由此求数列
是等差数列还是等比数列,并由此求数列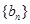 的通项公式;
的通项公式;
(Ⅱ)求数列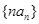 的前n项和
的前n项和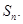
设x=1和x=2是函数f(x)=alnx+bx2+x的两个极值点
(1)求a,b的值;
(2)求f(x)的单调区间。
已知函数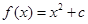 的图象经过点
的图象经过点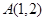 .
.
(1)求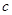 的值;
的值;
(2)求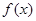 在
在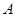 点处的切线方程.
点处的切线方程.
已知椭圆中心在原点,焦点在x轴上,离心率e= ,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
,它与直线x+y+1=0交于P、Q两点,若OP⊥OQ,求椭圆方程。(O为原点)。
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=
(1)求椭圆方程;
(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2。
某种汽车购买时费用为14.4万元,每年应交付保险费、养路费及汽油费共0.9万元,汽车的维修费为:第一年0.2万元,第二年0.4万元,第三年0.6万元,……,依等差数列逐年递增.
(Ⅰ)设使用n年该车的总费用(包括购车费用)为f(n),试写出f(n)的表达式;
(Ⅱ)求这种汽车使用多少年报废最合算(即该车使用多少年平均费用最少)。