某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
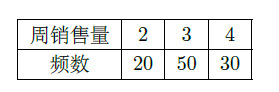
(Ⅰ)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(Ⅱ)已知每吨该商品的销售利润为2千元,
表示该种商品两周销售利润的和(单位:千元).若以上述频率作为概率,且各周的销售量相互独立,求
的分布列和数学期望.
(本小题12分)
某商店按每件80元的价格,购进时令商品(卖不出去的商品将成为废品)1000件;市场调研推知:当每件售价为100元时,恰好全部售完;在此基础上当售价每提高1元时,销售量就减少5件;为获得最大利润,请你确定合理的售价,并求出此时的利润;
(本小题12分)已知二次函数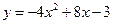 。
。
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3 )求函数的最大值或最小值;
)求函数的最大值或最小值;
(4)写出函数的单调区间(不必证明)。
(本小题12分)
设函数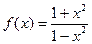
(1)求它的定义域和值域;(2)判断它的奇偶性;(3)求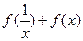 的值.
的值.
(本小题12分)
已知集合A=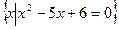 ,B=
,B=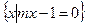 ,且
,且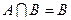 ,求由实数
,求由实数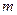 所构成的集合
所构成的集合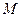 ,并写出
,并写出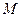 的所有子集。
的所有子集。
已知集合A={x| 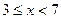 }, B={
}, B={ }, C={
}, C={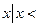 a}
a}
(1)求 (2)求
(2)求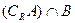 ;(3)若
;(3)若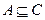 ,求a的取值范围.
,求a的取值范围.