已知椭圆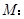
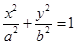 (
( ),点
),点
 、
、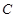
 分别是椭圆
分别是椭圆 的左焦点、左顶点,过点
的左焦点、左顶点,过点 的直线
的直线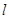 (不与
(不与 轴重合)交
轴重合)交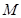 于
于 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若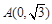 ,求△
,求△ 的面积;
的面积;
(3)是否存在直线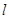 ,使得点
,使得点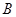 在以线段
在以线段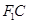 为直径的圆上,若存在,求出直线
为直径的圆上,若存在,求出直线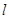 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知椭圆E的长轴长与焦距比为2:1,左焦点F(﹣2,0),一定点为P(﹣8,0).
(1)求椭圆E的标准方程;
(2)过P的直线与椭圆交于P1、P2两点,设直线P1F、P2F的斜率分别为k1、k2,求证:k1+k2=0.
(3)求△P1P2F面积的最大值.
已知二次函数f(x)=x2+x的定义域为D恰是不等式 的解集,其值域为A,函数g(x)=x3﹣3tx+
的解集,其值域为A,函数g(x)=x3﹣3tx+ 的定义域为[0,1],值域为B.
的定义域为[0,1],值域为B.
(1)求函数f(x)定义域为D和值域A;
(2)是否存在负实数t,使得A⊆B成立?若存在,求负实数t的取值范围;若不存在,请说明理由;
(3)若函数g(x)=x3﹣3tx+ 在定义域[0,1]上单调递减,求实数t的取值范围.
在定义域[0,1]上单调递减,求实数t的取值范围.
已知 =(cos2
=(cos2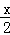 ,
,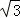 sinx),
sinx),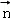 =(2,1),设函数f(x)=
=(2,1),设函数f(x)=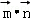 .
.
(1)当x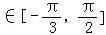 ,求函数f(x)的值域;
,求函数f(x)的值域;
(2)当f(α)= ,且﹣
,且﹣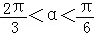 ,求sin(2
,求sin(2 )的值.
)的值.
已知函数f(x)=x2+|x﹣a|.
(1)当a=1时,求函数f(x)的最小值;
(2)试讨论函数f(x)的奇偶性,并说明理由.
公差不为零的等差数列{an}中,a1、a2、a5成等比数列,且该数列的前10项和为100.
(1)求数列{an}的通项公式;
(2)若bn=an﹣10,求数列{bn}的前n项和Tn的最小值.