已知椭圆E的长轴长与焦距比为2:1,左焦点F(﹣2,0),一定点为P(﹣8,0).
(1)求椭圆E的标准方程;
(2)过P的直线与椭圆交于P1、P2两点,设直线P1F、P2F的斜率分别为k1、k2,求证:k1+k2=0.
(3)求△P1P2F面积的最大值.
(本小题满分13分)
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:
(Ⅰ)连续取两次都是白球的概率;
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.
(本小题满分12分) 已知函数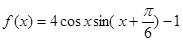
(Ⅰ)求 的最小正周期
的最小正周期
(Ⅱ)求在区间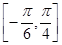 上的最值及相应
上的最值及相应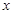 的值。
的值。
(本小题满分14分)设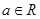 ,函数
,函数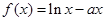 .
.
(1) 若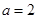 ,求曲线
,求曲线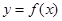 在
在 处的切线方程;
处的切线方程;
(2) 若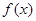 无零点,求实数
无零点,求实数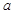 的取值范围;
的取值范围;
(3) 若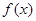 有两个相异零点
有两个相异零点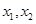 ,求证:
,求证: 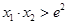 .
.
(本题满分14分
已知椭圆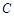 :
: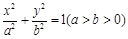 的离心率为
的离心率为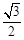 ,以原点为圆心,
,以原点为圆心,
椭圆的短半轴长为半径的圆与直线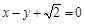 相切.
相切.
⑴求椭圆C的方程;
⑵设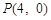 ,
,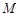 、
、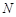 是椭圆
是椭圆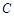 上关于
上关于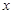 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结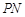 交椭圆
交椭圆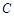
于另一点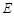 ,求直线
,求直线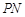 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线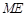 与
与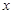 轴相交于定点.
轴相交于定点.
在数列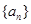 中,
中,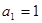 ,
,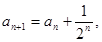 ,
,
(1)求数列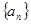 的通项公式;
的通项公式;
(2)求数列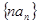 的前
的前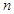 项和
项和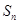 ;
;
(3)在(2)的条件下指出数列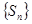 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。