设定义在R上的函数f（x）对于任意x，y都有f（x+y）=f（x）+f（y）成立，且f（1）=﹣2，当x＞0时，f（x）＜0．
（1）判断f（x）在R上的单调性，并加以证明；
（2）当﹣2015≤x≤2015时，不等式f（x）≤k恒成立，求实数k的取值范围．
一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：
，
，
，
，
，
．
（1）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；
（2）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望．
已知命题p：关于x的方程x2+ax+a=0有实数解；命题q：﹣1＜a≤2．
（1）若¬p是真命题，求实数a的取值范围；
（2）若（¬p）∧q是真命题，求实数a的取值范围．
甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为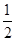
与p，且乙投球2次均未命中的概率为
．
（Ⅰ）求乙投球的命中率p；
（Ⅱ）求甲投球2次，至少命中1次的概率；
（Ⅲ）若甲、乙两人各投球2次，求两人共命中2次的概率．
已知函数
，
，
．
（1）当
时，求函数
的单调区间；
（2）若函数在区间
上的最小值是
，求
的值；
（3）设
是函数
图象上任意不同的两点，线段
的中点为
，直线的斜率为
，证明：
.