在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线 ,已知过点
,已知过点 的直线的参数方程为:
的直线的参数方程为: (t为参数),直线与曲线C分别交于M,N.
(t为参数),直线与曲线C分别交于M,N.
(Ⅰ)写出曲线C和直线的普通方程;
(Ⅱ)若 成等比数列,求a的值.
成等比数列,求a的值.
已知
(1)若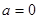 时,求函数
时,求函数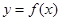 在点
在点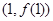 处的切线方程;
处的切线方程;
(2)若函数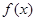 在
在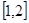 上是减函数,求实数
上是减函数,求实数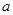 的取值范围;
的取值范围;
(3)令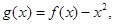 是否存在实数
是否存在实数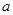 ,当
,当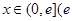 是自然对数的底)时,函数
是自然对数的底)时,函数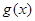 的最小值是3,
的最小值是3,
若存在,求出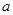 的值;若不存在,说明理由.
的值;若不存在,说明理由.
设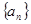 是正数组成的数列,
是正数组成的数列, .若点
.若点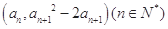 在函数
在函数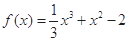 的导函数
的导函数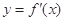 图像上.
图像上.
(1)求数列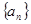 的通项公式;
的通项公式;
(2)设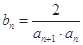 ,是否存在最小的正数
,是否存在最小的正数 ,使得对任意
,使得对任意
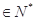 都有
都有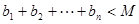 成立?请说明理由.
成立?请说明理由.
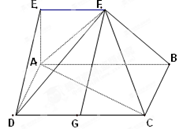
如图,在多面体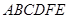 中,四边形
中,四边形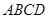 是矩形,
是矩形,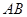 ∥
∥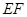 ,
,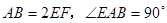 ,平面
,平面 .
.
(1)若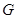 点是
点是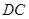 中点,求证:
中点,求证: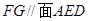 .
.
(2)求证: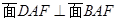 .
.
(3)若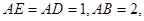 求
求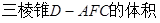 .
.
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组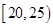 ,第2组
,第2组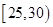 ,第3组
,第3组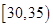 ,第4组
,第4组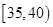 ,第5组
,第5组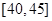 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
已知向量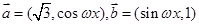
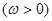 ,函数
,函数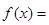
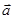 ·
·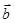 ,且最小正周期为
,且最小正周期为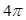 .
.
(1)求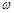 的值;
的值;
(2)设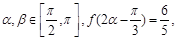
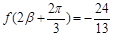 ,求
,求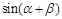 的值.
的值.