(本小题满分14分)如图,已知四棱锥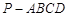 中,底面
中,底面 为矩形,侧棱
为矩形,侧棱 ,
, 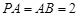 ,
,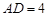 ,
, 为侧棱
为侧棱 的中点.
的中点.
(1)求异面直线 与
与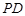 所成角的余弦值;
所成角的余弦值;
(2)求二面角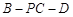 的余弦值.
的余弦值.
16. (本小题满分13分)
设集合 ,若
,若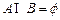 ,求实数a的取值范围.
,求实数a的取值范围.
21.(本小题满分13分)
设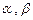 是函数
是函数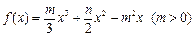 的两个极值点,且
的两个极值点,且 .
.
(1)求证: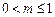 ;
;
(2)求 的取值范围;
的取值范围;
(3)若函数 ,当
,当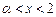 且
且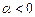 时,求证:
时,求证: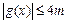 .
.
20.(本小题满分13分)
已知数列{an}有a1 = a,a2 = p(常数p > 0),对任意的正整数n,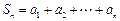 ,且
,且 .
.
(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式;若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b,使得对任意的正整数n都有bn< b,且 ,则称b为数列{bn}的“上渐近值”,令
,则称b为数列{bn}的“上渐近值”,令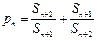 ,求数列
,求数列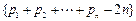 的“上渐近值”.
的“上渐近值”.
(本小题满分14分)一束光线 通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线
通过点M(-3,3)射到x轴上,然后反射到圆C上,其中圆C满足以下条件:过点A(1,2)和点B(2,3)且圆心在直线 上。
上。
(1)求圆C的方程;
(2)求通过圆C圆心的反射光线所在直线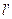 的方程;
的方程;
(3)若反射光线所在直线与圆C相切,求入射光线所在直线 的方程
的方程
(本小题满分12分)求与x轴相切,圆心在直线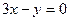 上,且被直线
上,且被直线 截得的弦长为
截得的弦长为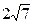 的圆的方程。
的圆的方程。