已知函数 ,求导函数 ,并确定 的单调区间.
(1) 求内接于半径为R的球并且体积最大的圆柱的高.
(2) 求内接于半径为R的球并且体积最大的圆锥的高.
如图,将边长为a的正方形铁皮的四角各截去一个同样大小的小正方形后,将四边向上翻折做成一个无盖的正四棱柱形容器,求此容器的体积最大值. 
(本小题满分15分)已知函数 .
.
(1)若函数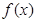 的值域为
的值域为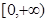 ,求a的值;
,求a的值;
(2)若函数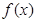 在
在 上是增函数,求实数
上是增函数,求实数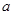 的取值范围.
的取值范围.
(本小题满分15分)定义在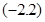 上的奇函数
上的奇函数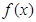 ,满足
,满足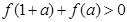 ,又当
,又当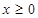 时,
时,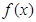 是减函数,求
是减函数,求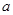 的取值范围。
的取值范围。
(本小题满分15分)将进货单价为80元的商品按90元一个售出时,能卖出400个,已知这种商品每个涨价1元,其销售量就减少10个,为了取得最大利润,每个售价应定为多少元?