(1) 求内接于半径为R的球并且体积最大的圆柱的高.
(2) 求内接于半径为R的球并且体积最大的圆锥的高.
某单位组织4个部门的职工旅游,规定每个部门只能在峨眉山、泰山、华山3个景区中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率.
设数列 的前
的前 项和为
项和为 ,已知
,已知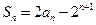 (n∈N*).
(n∈N*).
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设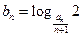 ,数列
,数列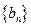 的前
的前 项和为
项和为 ,若存在整数
,若存在整数 ,使对任意n∈N*且n≥2,都有
,使对任意n∈N*且n≥2,都有 成立,求
成立,求 的最大值;
的最大值;
(Ⅲ)令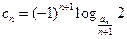 ,数列
,数列 的前
的前 项和为
项和为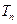 ,求证:当n∈N*且n≥2时,
,求证:当n∈N*且n≥2时, .
.
如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放. 根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.
(Ⅰ)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m3,试根据环保部门的要求写出x、y所满足的所有条件;
(Ⅱ)已知甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,在满足环保部门要求的条件下,甲、乙两个化工厂每天应分别各自处理污水多少万m3,才能使这两个工厂处理污水的总费用最小?最小总费用是多少元? 
设向量a=(x+1,y),b=(x-1,y),点P(x,y)为动点,已知|a|+|b|=4.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点P的轨迹与x轴负半轴交于点A,过点F(1,0)的直线交点P的轨迹于B、C两点,试推断△ABC的面积是否存在最大值?若存在,求其最大值;若不存在,请说明理由.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.
(Ⅰ)判断平面ADE与平面BCE是否垂直,并说明理由;
(Ⅱ)求点D到平面ACE的距离. 