如图,某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂,其中甲厂每天向河道内排放污水2万m3,每天流过甲厂的河水流量是500万m3(含甲厂排放的污水);乙厂每天向河道内排放污水1.4万m3,每天流过乙厂的河水流量是700万m3(含乙厂排放的污水).由于两厂之间有一条支流的作用,使得甲厂排放的污水在流到乙厂时,有20%可自然净化.假设工厂排放的污水能迅速与河水混合,且甲厂上游及支流均无污水排放. 根据环保部门的要求,整个河流中污水含量不能超过0.2%,为此,甲、乙两个工厂都必须各自处理一部分污水.
(Ⅰ)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m3,试根据环保部门的要求写出x、y所满足的所有条件;
(Ⅱ)已知甲厂处理污水的成本是1200元/万m3,乙厂处理污水的成本是1000元/万m3,在满足环保部门要求的条件下,甲、乙两个化工厂每天应分别各自处理污水多少万m3,才能使这两个工厂处理污水的总费用最小?最小总费用是多少元? 
(本小题满分12分)某班同学利用国庆节进行社会实践,对 [25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
(1)补全频率分布直方图并求n、a、p的值;
(2)从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和期望E(X).
(本小题满分12分)在三棱锥M-ABC中,AB=2AC=2,MA=MB= ,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
,AB=4AN,AB^AC,平面MAB^平面ABC,S为BC的中点.
(1)证明:CM^SN;
(2)求SN与平面CMN所成角的大小.
(本小题满分12分)在△ABC中,已知asinA-csinC=(a-b)sinB, △ABC外接圆的半径为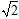 .
.
(1)求C;
(2)求△ABC的面积S的最大值.
已知函数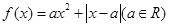 .
.
(1)当 时,写出
时,写出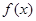 的单调区间;
的单调区间;
(2)当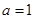 时,求
时,求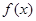 的最小值;
的最小值;
(3)试讨论关于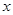 的方程
的方程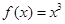 的解的个数.
的解的个数.
解关于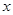 的不等式:
的不等式: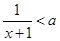 .
.