某单位组织4个部门的职工旅游，规定每个部门只能在峨眉山、泰山、华山3个景区中任选一个，假设各部门选择每个景区是等可能的.
（Ⅰ）求3个景区都有部门选择的概率；
（Ⅱ）求恰有2个景区有部门选择的概率.
已知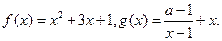
（I）a=2时，求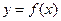
和
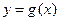的公共点个数；
（II）a为何值时，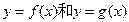
的公共点个数恰为两个。
已知椭圆
的右焦点为F2（1，0），点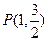
在椭圆上。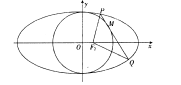
（I）求椭圆方程；
（II）点
在圆
上，M在第一象限，过M作圆的切线交椭圆于P、Q两点，问|F2P|+|F2Q|+|PQ|是否为定值？如果是，求出定值，如不是，说明理由。
已知数列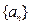
的前n项和为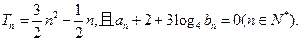
（I）求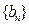
的通项公式；
（II）数列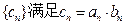
，求数列
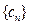的前n项和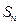
；
（III）若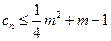
对一切正整数n恒成立，求实数m的取值范围。
如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，点F在CE上，且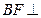
平面ACE。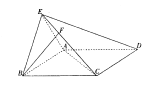
（I）求证：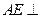
平面BCE；
（II）求二面角B—AC—E的正弦值；
（III）求点D到平面ACE的距离。
某种植企业同时培育甲、乙两个品种杉树幼苗，甲品种杉树幼苗培育成功则每株利润80元，培育失败，则每株亏损20元；乙品种杉树幼苗培育成功则每株获利润150元，培育失败，则每株亏损50元。统计数据表明：甲品种杉树幼苗培育成功率为90%，乙品种杉树幼苗培育成功率为80%。假设每株幼苗是否培育成功相互独立。
（I）求培育3株甲品种杉树幼苗成功2株的概率；
（II）记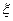
为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润，求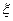的分布列及其期望。