(本小题13分)已知数列{an}的前n项和Sn = 2an– 3×2n + 4 (n∈N*)
(1)求数列{an}的通项公式an;(2)设Tn为数列{Sn – 4}的前n项和,试比较Tn与14的大小.
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?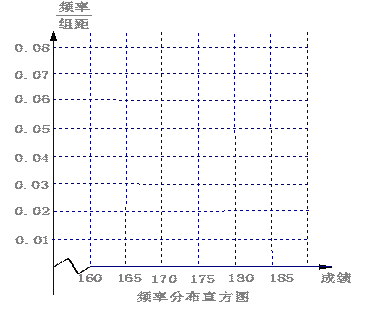
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
 |
30 |
② |
| 第4组 |
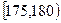 |
20 |
0.200 |
| 第5组 |
 |
10 |
0.100 |
| 合计 |
100 |
1.000 |
|
(本小题满分12分)
如图某河段的两岸可视为平行,为了测量该河段的宽度,在河段的一岸边选取两点A、B,观察对岸的点C,测得 ,
, ,且
,且 米。
米。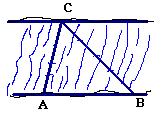
(1)求 ;
;
(2)求该河段的宽度。
已知
(I)求 的值;
的值;
(II)求 ;
;
(III)求证:
 已知两点M、N分别在直线
已知两点M、N分别在直线 与直线
与直线 上运动,且|MN|=2.动点P满足
上运动,且|MN|=2.动点P满足 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.
(I)求曲线C的方程;
(II)过点(0,1)作直线l与曲线C交于不同的两点A、B.若对任意 ,都有∠AOB为锐角,求直线l的斜率k的取值范围.
,都有∠AOB为锐角,求直线l的斜率k的取值范围.
如图,四棱锥P—ABCD的底面为矩形,PA=AD=1,PA⊥面ABCD,E是AB的中点,F为PC上一点,且EF//面PAD。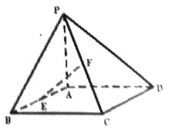
(I)证明:F为PC的中点;
(II)若二面角C—PD—E的平面角的余弦值为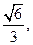 求直线ED与平面PCD所成的角
求直线ED与平面PCD所成的角