 已知两点M、N分别在直线
已知两点M、N分别在直线 与直线
与直线 上运动,且|MN|=2.动点P满足
上运动,且|MN|=2.动点P满足 (O为坐标原点),点P的轨迹记为曲线C.
(O为坐标原点),点P的轨迹记为曲线C.
(I)求曲线C的方程;
(II)过点(0,1)作直线l与曲线C交于不同的两点A、B.若对任意 ,都有∠AOB为锐角,求直线l的斜率k的取值范围.
,都有∠AOB为锐角,求直线l的斜率k的取值范围.
(本小题满分15分)已知函数
 且
且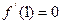 .
.
(Ⅰ)试用含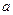 式子表示
式子表示 ;(Ⅱ)求
;(Ⅱ)求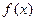 的单调区间;(Ⅲ)若
的单调区间;(Ⅲ)若 ,试求
,试求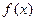 在区间
在区间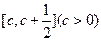 上的最大值.
上的最大值.
已知数列 的前n项和为
的前n项和为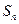 ,对任意的
,对任意的 ,点
,点 ,均在函数
,均在函数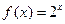 的图像上.(Ⅰ)求数列
的图像上.(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,求使
,求使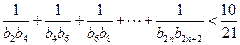 成立的
成立的 的最大值.
的最大值.
已知向量  ,
, ,函数
,函数 。(Ⅰ)求
。(Ⅰ)求 的最小正周期;(II)若
的最小正周期;(II)若 ,求
,求 的值域.
的值域.
已知菱形 的边长为2,对角线
的边长为2,对角线 与
与 交于点
交于点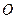 ,且
,且 ,
,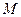 为
为 的中点.将此菱形沿对角线
的中点.将此菱形沿对角线 折成直二面角
折成直二面角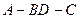 .
.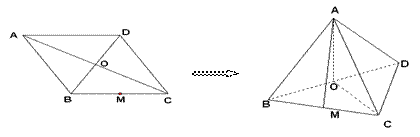
(I)求证: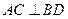 ;
;
(II)求直线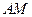 与面
与面 所成角的余弦值大小.
所成角的余弦值大小.
已知函数
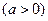 且导数
且导数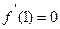 .
.
(Ⅰ)试用含有 的式子表示
的式子表示 ,并求
,并求 单调区间;(II)对于函数图象上的不同两点
单调区间;(II)对于函数图象上的不同两点 ,如果在函数图象上存在点
,如果在函数图象上存在点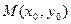 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称
,则称 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当 时,又称
时,又称 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数 上是否存在两点
上是否存在两点 、
、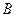 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出 、
、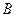 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.