某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六段[40，50），[50，60）， ，[90，100]后画出如下部分频率分布直方图．观察图形给出的信息，回答下列问题：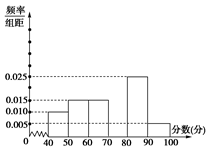
（1）求第四小组的频率，并补全这个频率分布直方图；
（2）估计这次考试的及格率（60分及以上为及格）和平均分；
（3）从成绩是[40，50）和[90，100]的学生中选两人，求他们在同一分数段的概率．
已知椭圆E的长轴的一个端点是抛物线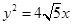
的焦点，离心率是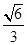
（1）求椭圆E的方程；
（2）过点C（—1，0），斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使
为常数？若存在，求出点M的坐标；若不存在，请说明理由。
已知圆C：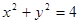
和直线l：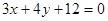
，点P是圆C上的一动点，直线与坐标轴的交点分别为点A、B，
（1）求与圆C相切且平行直线l的直线方程；
（2）求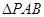
面积的最大值。
（本小题满分14分）已知定义在正实数集上的函数f（x）＝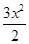
＋ax，g（x）＝4a2lnx＋b，其中a＞0，设两曲线y＝f（x）与y＝g（x）有公共点，且在公共点处的切线相同.
（1）若a＝1，求两曲线y＝f（x）与y＝g（x）在公共点处的切线方程；
（2）用a表示b，并求b的最大值.
（本小题满分13分）如图，点M（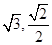
）在椭圆
（a＞b＞0）上，且点M到两焦点的距离之和为4.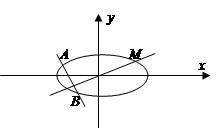
（1）求椭圆方程；
（2）设与MO（O为坐标原点）垂直的直线交椭圆于A、B（A、B不重合），求
的取值范围.
（本小题满分12分）已知数列{an}满足an＝2an－1＋2n＋1（n∈N，n＞1），a3＝27，数列{bn}满足bn＝
（an＋t）.
（1）若数列{bn}为等差数列，求bn；
（2）在（1）的条件下，求数列{an}的前n项和Sn.