(本小题满分16分)
在数列 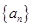 中,已知
中,已知 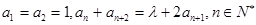 ,
, 为常数.
为常数.
(1)证明: 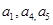 成等差数列;
成等差数列;
(2)设  ,求数列 的前n项和
,求数列 的前n项和 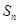 ;
;
(3)当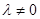 时,数列
时,数列 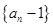 中是否存在三项
中是否存在三项 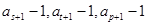 成等比数列,且
成等比数列,且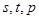 也成等比数列?若存在,求出
也成等比数列?若存在,求出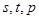 的值;若不存在,说明理由.
的值;若不存在,说明理由.
如图,抛物线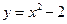 与圆
与圆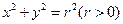 相交于
相交于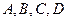 四个不同点。
四个不同点。
(Ⅰ)求半径 的取值范围;(Ⅱ)求四边形
的取值范围;(Ⅱ)求四边形 面积的最大值。
面积的最大值。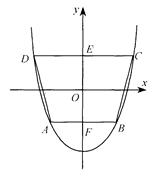
设函数 有两个极值点
有两个极值点 ,且满足:
,且满足: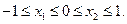
(Ⅰ)求动点 移动所形成的区域的面积;(Ⅱ)当
移动所形成的区域的面积;(Ⅱ)当 变化时,求
变化时,求 极大值的取值范围。
极大值的取值范围。
规定记号“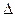 ”表示一种运算,即
”表示一种运算,即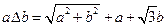 ,
,
记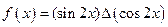 .
.
(1)求函数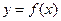 的表达式;
的表达式;
(2)求函数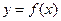 的最小正周期;
的最小正周期;
(3)若函数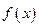 在
在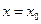 处取到最大值,求
处取到最大值,求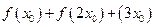 的值.
的值.
某商店经销一种奥运纪念品,据预测,在元旦后的20天内的每天销售量(件)与价格(元)均为时间t(天)的函数,且第t天的销售量近似满足g(t)=80-2t(件),第t天的价格近似满足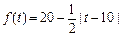 (元).
(元).
(1)试写出该纪念品的日销售额y与时间t(0≤t≤20)的函数关系式;
(2)求该纪念品的日销售额y的最大值与最小值.
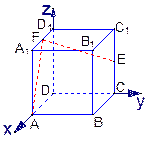
棱长为2的正方体A1B1C1D1-ABCD中,E、F分别是C1C和D1A1的中点,
(1)求异面直线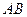 与
与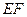 所成的角的余弦值;
所成的角的余弦值;
(2)求点A到EF的距离.