（本小题满分12分）
2008年为山东素质教育年，为响应素质教育的实施，某中学号召学生在放假期间至少参加一次社会实践活动（以下简称活动）．现统计了该校100名学生参加活动的情况，他们参加活动的次数统计如图所示．
（1）求这些学生参加活动的人均次数；
（2）从这些学生中任选两名学生，求他们参加活动次数恰好相等的概率；
（3）从这些学生中任选两名学生，用
表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望
．
如图，在三棱锥
中，侧面
与侧面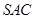
均为等边三角形，
，
为
中点．
（Ⅰ）证明：
平面
；
（Ⅱ）求二面角
的余弦值．（本题12分）
在
的展开式中，求：（1）第5项的二项式系数;（2）第5项的系数;（3）倒数第3项;（4）含
的项。 （本题12分）
如图所示，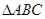
是等腰直角三角形，
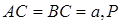是 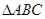所在平面外一点，
（1）求证：面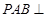
面
；
（2）求
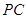和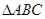所在平面所成角。（本题12分）
已知9个外语教师，4人只会英语，3人只会日语，另外2人既会英语又会日语，从中选4人，2人教英语，2人教日语，有多少种不同安排方案？（本题12分）
在空间四边形ABCD中，已知AC=2，BD=2，E、F分别为AD、BC中点，且EF=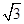
，
求AC和BD所成的角。（本题12分）