(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数: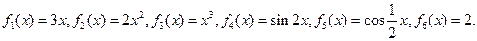
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是偶函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有奇函数的卡片则停止抽取,否则继续进行. 求抽取次数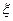 的分布列、数学期望和方差.
的分布列、数学期望和方差.
已知实数组成的数组 满足条件:
满足条件:
① ;②
;② .
.
(Ⅰ)当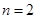 时,求
时,求 ,
,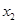 的值;
的值;
(Ⅱ)当 时,求证:
时,求证: ;
;
(Ⅲ)设 ,且
,且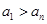
 ,求证:
,求证: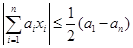 .
.
设 是曲线
是曲线 上的任一点,
上的任一点, 是曲线
是曲线 上的任一点,称
上的任一点,称 的最小值为曲线
的最小值为曲线 与曲线
与曲线 的距离.
的距离.
(1)求曲线 与直线
与直线 的距离;
的距离;
(2)设曲线 与直线
与直线 (
( )的距离为
)的距离为 ,直线
,直线 与直线
与直线 的距离为
的距离为 ,求
,求 的最小值.
的最小值.
如图,边长为2的正方形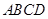 中,点
中,点 是
是 的中点,点
的中点,点 是
是 的中点,将△
的中点,将△ 、△
、△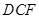 分别沿
分别沿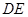 、
、 折起,使
折起,使 、
、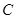 两点重合于点
两点重合于点 ,连接
,连接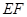 ,
, .
.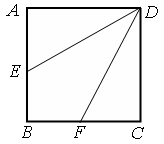

(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
已知数列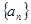 的前
的前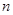 项和为
项和为 ,数列
,数列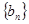 的首项
的首项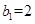 ,且点
,且点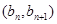 在直线
在直线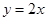 上.
上.
(1)求数列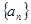 ,
,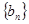 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前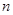 项和
项和 .
.
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.