(本题满分12分)如图,四棱锥P—ABCD中,PA⊥ABCD,四边形ABCD 是矩形. E、F分别是AB、PD的中点.若PA=AD=3,CD= . (1)求证:AF//平面PCE;
. (1)求证:AF//平面PCE;

(2)求点A到平面PCE的距离;(3)求直线FC与平面PCE所成角的大小。
某个车间工人已加工一种轴 件,为了了解这种轴的直径,要从中抽出
件,为了了解这种轴的直径,要从中抽出 件在同一条件下测量,如何采用简单随机抽样的方法抽取上述样本?
件在同一条件下测量,如何采用简单随机抽样的方法抽取上述样本?
设数列 满足
满足 ,
,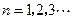 ,
,
(1)当 时,求
时,求 ,并由此猜想出
,并由此猜想出 的一个通项公式;
的一个通项公式;
(2)当 时,证明对所有的
时,证明对所有的 ,有
,有
① ;②
;② .
.
把10个运动队先均分成两组进行预赛.
(1)求最强两队被分在不同组内的概率;
(2)求最强两队被分在同一组内的概率.
为了保护环境,某校环保小组成员小沅收集废电池,第一天收集 号电池
号电池 节,
节, 号电池
号电池 节,总质量为
节,总质量为 ;第二天收集
;第二天收集 号电池
号电池 节,
节, 号电池
号电池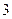 节,总质量为
节,总质量为 .
.
(1)求 号电池和
号电池和 号电池每节质量各为多少克?
号电池每节质量各为多少克?
(2)学校环保小组为估计四月份收集电池的总质量,随机抽取了该月某 天收
天收
集废电池的节数如下表:
 号废电池(单位:节) 号废电池(单位:节) |
 |
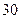 |
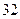 |
 |
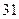 |
 号废电池(单位:节) 号废电池(单位:节) |
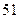 |
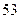 |
 |
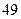 |
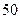 |
分别计算这 天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?
天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?
乙两个小组各 名学生的英语口语测试成绩如下(单位:分):
名学生的英语口语测试成绩如下(单位:分):
甲组: ;
;
乙组: .
.
试分析哪个小组学生的成绩比较整齐?